题目内容
【题目】设函数f（x）=2ax2+（a+4）x+lnx．
（1）若f（x）在x= 
处的切线与直线4x+y=0平行，求a的值；
（2）讨论函数f（x）的单调区间；
（3）若函数y=f（x）的图象与x轴交于A，B两点，线段AB中点的横坐标为x0 ， 证明f′（x0）＜0．
【答案】
（1）解：由题知f（x）=2ax2+（a+4）x+lnx，
则 
．
又∵f（x）的图象在x= 
处的切线与直线4x+y=0平行，
∴ 
，即4a× 
+ ×（a+4）+1=﹣1，
解得 a=﹣6．
（2）解：由（1）得， 
，
由题知f（x）=2ax2+（a+4）x+lnx的定义域为（0，+∞），
由x＞0，得 
＞0．
①当a≥0时，对任意x＞0，f′（x）＞0，
∴此时函数f（x）的单调递增区间为（0，+∞）．
②当a＜0时，令f′（x）=0，解得 
，
当 
时，f′（x）＞0，当 
时，f′（x）＜0，
此时，函数f（x）的单调递增区间为（0， 
），单调递减区间为（ ，+∞）．
（3）解：不妨设A（x1，0），B（x2，0），且0＜x1＜x2，由（Ⅱ）知 a＜0，
于是要证f'（x）＜0成立，只需证： 
即 
．
∵ 
，①
，②
①﹣②得 
，
即 
，
∴ 
，
故只需证 
，
即证明 
，
即证明 
，变形为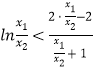 
，
设 
（0＜t＜1），令 
，
则 
= 
，
显然当t＞0时，g′（t）≥0，当且仅当t=1时，g′（t）=0，
∴g（t）在（0，+∞）上是增函数．
又∵g（1）=0，
∴当t∈（0，1）时，g（t）＜0总成立，命题得证
【解析】（1）利用求导公式求出导数并化简，由导数的几何意义和题意可得f′（ 
）=﹣4，解出a的值即可；（2）对导数因式分解后，再求出函数f（x）的定义域，然后在定义域内分a≥0，a＜0两种情况，解不等式f′（x）＞0，f′（x）＜0可得函数的单调区间；（3）设出函数y=f（x）的图象与x轴交于A，B两点的横坐标，利用分析法和根据（2）结论进行证明，根据要证明的结论和分析的过程，利用放缩法、换元法、构造函数法解答，再利用导数求出函数的最值，即可证明结论．
【考点精析】根据题目的已知条件，利用利用导数研究函数的单调性的相关知识可以得到问题的答案，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减．
