Question

【题目】已知a>0，a≠1，设p：函数y＝loga(x＋3)在(0，＋∞)上单调递减，q：函数y＝x2＋(2a－3)x＋1的图像与x轴交于不同的两点．如果p∨q真，p∧q假，求实数a的取值范围．

Answer 1

【答案】[，1)∪(，＋∞)．

【解析】

先求出当命题p，q为真命题时的取值范围，由p∨q真，p∧q假可得p与q一真一假，由此可得关于的不等式组，解不等式组可得结论．

当命题p为真，即函数y＝loga(x＋3)在(0，＋∞)上单调递减时，

可得．

当命题q为真，即函数y＝x2＋(2a－3)x＋1的图像与x轴交于不同的两点，

可得，

解得，

又，

所以当q为真命题时，有．

∵p∨q为真，p∧q为假，

∴p与q一真一假．

①若p真q假，则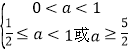 ，解得；

②若p假q真，则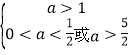 ，解得．

综上可得或．

∴实数a的取值范围是[，1)∪(，＋∞)．