题目内容
【题目】已知数列{bn}的前n项和 
．
（1）求数列{bn}的通项公式；
（2）设数列{an}的通项 
，求数列{an}的前n项和Tn ．
【答案】
（1）解：∵数列{bn}的前n项和 
，∴b1=B1= 
=1；
当n≥2时，bn=Bn﹣Bn﹣1= 
﹣ 
=3n﹣2，当n=1时也成立．
∴bn=3n﹣2．
（2）解： 
=（3n﹣2）2n+（﹣1）n2n．
设数列{（3n﹣2）2n}的前n项和为An，
则An=2+4×22+7×23+…+（3n﹣2）2n，
2An=22+4×23+…+（3n﹣5）2n+（3n﹣2）2n+1，
∴﹣An=2+3（22+23+…+2n）﹣（3n﹣2）2n+1= 
﹣4﹣（3n﹣2）2n+1=（5﹣3n）2n+1﹣10，
∴An=（3n﹣5）2n+1+10．
数列{（﹣1）n2n}的前n项和= 
= 
[1﹣（﹣2）n]．
∴数列{an}的前n项和Tn=（3n﹣5）2n+1+10 [1﹣（﹣2）n]
【解析】（1）利用递推关系即可得出；（2） =（3n﹣2）2n+（﹣1）n2n ． 设数列{（3n﹣2）2n}的前n项和为An ， 利用“错位相减法”与等比数列的前n项和公式即可得出；再利用等比数列的前n项和公式即可得出．
【考点精析】根据题目的已知条件，利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系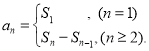
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
【题目】某种子培育基地新研发了
两种型号的种子，从中选出90粒进行发芽试验，并根据结果对种子进行改良.将试验结果汇总整理绘制成如下
列联表：
（1）将列联表补充完整，并判断是否有99%的把握认为发芽和种子型号有关；
（2）若按照分层抽样的方式，从不发芽的种子中任意抽取20粒作为研究小样本，并从这20粒研究小样本中任意取出3粒种子，设取出的
型号的种子数为
，求的分布列与期望.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
，其中
.
