题目内容

【题目】已知函数.

⑴判断的奇偶性.

⑵写出的单调区间(只需写出结果).

⑶若方程有解，求实数的取值范围.

【答案】(1)奇函数;(2) 函数的单调递减区间为:,;单调递增区间为:,;(3)

【解析】

(1)利用奇偶函数的定义 和判断可得;

(2)先写出时函数的单调区间,再根据函数的奇偶性得到时的单调区间;

(3)将方程有解转化为函数 与函数 的图象有交点,作出图象后,观察图象可得.

(1)因为的定义域为R,

,所以,

所以函数为偶函数.

(2)当时,在上递减,在上递增,

又因为函数为偶函数,所以在上递减,在上递增,

故函数的单调递减区间为:,;单调递增区间为:,.

(3)因为方程有解,所以函数与函数的图象有交点,

作出函数的图象如下:

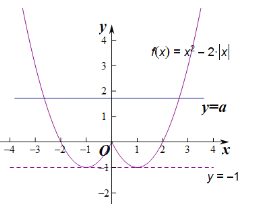
由图可知:.

所以实数的取值范围是.

练习册系列答案
相关题目

【题目】已知集合A={x|3≤x<7},B={x|2<x<10},C={x|x<a},全集U=R

(1)求A∪B;

(2)若,求实数a的取值范围

【题目】若不等式（1－a）x2－4x＋6>0的解集是{x|－3<x<1}．

（1）解不等式2x2＋（2－a）x－a>0；

（2）b为何值时，ax2＋bx＋3≥0的解集为R.

【题目】已知函数f(x)的定义域是{x|x≠0}，对定义域内的任意，都有f(·)＝f()＋f()，且当x>1时，f(x)>0，f(2)＝1.

(1)证明：(x)是偶函数；

(2)证明：(x)在(0，＋∞)上是增函数；

(3)解不等式(2－1)<2.

【题目】如图，AB是⊙O的直径，C，F是⊙O上的两点，OC⊥AB，过点F作⊙O的切线FD交AB的延长线于点D．连接CF交AB于点E．

（1）求证：DE2=DBDA；
（2）若DB=2，DF=4，试求CE的长．

【题目】已知两直线l1：ax－by＋4＝0，l2：(a－1)x＋y＋b＝0．求分别满足下列条件的a，b的值：

(1)直线l1过点(－3，－1)，并且直线l1与l2垂直；则a＝____，b＝_______

(2)直线l1与直线l2平行，并且直线l2在y轴上的截距为3．则a＝____，b＝_______

【题目】某种子培育基地新研发了两种型号的种子，从中选出90粒进行发芽试验，并根据结果对种子进行改良.将试验结果汇总整理绘制成如下列联表：

（1）将列联表补充完整，并判断是否有99%的把握认为发芽和种子型号有关；

（2）若按照分层抽样的方式，从不发芽的种子中任意抽取20粒作为研究小样本，并从这20粒研究小样本中任意取出3粒种子，设取出的型号的种子数为，求的分布列与期望.

0.15

0.10

0.05

0.025

0.010

0.005

0.001

2.072

2.706

3.841

5.024

6.635

7.879

10.828

，其中.

【题目】设函数f（x）=2ax2+（a+4）x+lnx．
（1）若f（x）在x= 处的切线与直线4x+y=0平行，求a的值；
（2）讨论函数f（x）的单调区间；
（3）若函数y=f（x）的图象与x轴交于A，B两点，线段AB中点的横坐标为x0 ， 证明f′（x0）＜0．

【题目】某闯关游戏规则是：先后掷两枚骰子，将此试验重复n轮，第n轮的点数分别记为xn ， yn ， 如果点数满足xn＜ ，则认为第n轮闯关成功，否则进行下一轮投掷，直到闯关成功，游戏结束．
（Ⅰ）求第一轮闯关成功的概率；
（Ⅱ）如果第i轮闯关成功所获的奖金数f（i）=10000× （单位：元），求某人闯关获得奖金不超过1250元的概率；
（Ⅲ）如果游戏只进行到第四轮，第四轮后不论游戏成功与否，都终止游戏，记进行的轮数为随机变量X，求x的分布列和数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网