题目内容
【题目】过抛物线![]() 的对称轴上一点
的对称轴上一点![]() 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() 、
、![]() .
.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)记![]()
![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() ,是否存在
,是否存在![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立.若存在,求
成立.若存在,求![]() 值;若不在,说明理由.
值;若不在,说明理由.
【答案】(Ⅰ)略
(Ⅱ)存在![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立,证明略
成立,证明略
【解析】
解:
依题意,可设直线MN的方程为![]() ,则有
,则有
![]()
由![]() 消去x可得
消去x可得![]()
从而有![]() ①
①
于是![]() ②
②
又由![]() ,
,![]() 可得
可得![]() ③
③
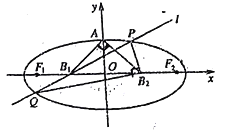
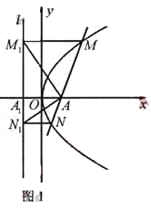
(Ⅰ)如图1,当![]() 时,点
时,点![]() 即为抛物线的焦点,
即为抛物线的焦点,![]() 为其准线
为其准线![]()
此时![]() ①可得
①可得![]()
证法1:![]()
![]()
证法2:![]()
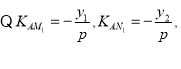
![]()
(Ⅱ)存在![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立,证明如下:
成立,证明如下:
证法1:记直线![]() 与x轴的交点为
与x轴的交点为![]() ,则
,则![]() .于是有
.于是有

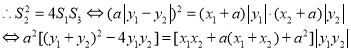
将①、②、③代入上式化简可得
![]()
上式恒成立,即对任意![]() 成立
成立
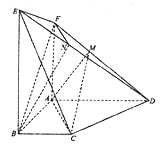
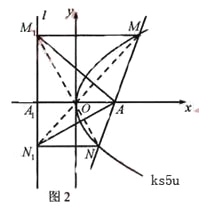
证法2:如图2,连接![]() ,则由
,则由![]() 可得
可得
![]() ,
,
所以直线![]() 经过原点O,同理可证直线
经过原点O,同理可证直线![]() 也经过原点O
也经过原点O
又![]() 设
设![]()
则![]()

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】现有一环保型企业,为了节约成本拟进行生产改造,现将某种产品产量![]() 与单位成本
与单位成本![]() 统计数据如下:
统计数据如下:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
产量(千件) | 2 | 3 | 4 | 5 | 4 | 5 |
单位成本(元/件) | 73 | 72 | 71 | 73 | 69 | 68 |
(Ⅰ)试确定回归方程![]() ;
;
(Ⅱ)指出产量每增加1000件时,单位成本平均下降多少?
(Ⅲ)假定单位成本为70元/件时,产量应为多少件?
(参考公式: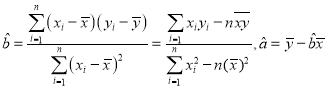 .)
.)
(参考数据![]()
![]() )
)
【题目】全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:
空气质量指数( | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;

(2)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.