题目内容
【题目】已知抛物线![]() ,M为直线
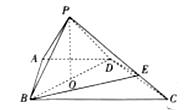
,M为直线![]() 上任意一点,过点M作抛物线C的两条切线MA,MB,切点分别为A,B.
上任意一点,过点M作抛物线C的两条切线MA,MB,切点分别为A,B.![]()
(1)当M的坐标为(0,-1)时,求过M,A,B三点的圆的方程; ![]()
(2)证明:以![]() 为直径的圆恒过点M.
为直径的圆恒过点M.
【答案】(1)![]() (2)见证明
(2)见证明
【解析】
(1)设出过![]() 点的切线方程,与抛物线方程联立,得到一个元二次方程,它的判别式为零,可以求出切线方程的斜率,这样可以求出A,B两点的坐标,设出圆心
点的切线方程,与抛物线方程联立,得到一个元二次方程,它的判别式为零,可以求出切线方程的斜率,这样可以求出A,B两点的坐标,设出圆心![]() 的坐标为
的坐标为![]() ,由
,由![]() ,可以求出
,可以求出![]() ,最后求出圆的方程;
,最后求出圆的方程;
(2)设![]() ,设切点分别为
,设切点分别为![]() ,
,![]() ,把抛物线方程化
,把抛物线方程化![]() ,求导,这样可以求出切线的斜率,求出切线
,求导,这样可以求出切线的斜率,求出切线![]() 的方程,切线
的方程,切线![]() 的方程,又因为切线
的方程,又因为切线![]() 过点
过点![]() ,切线
,切线![]() 也过点
也过点![]() ,这样可以发现
,这样可以发现![]() ,
,![]() 是一个关于
是一个关于![]() 的一元二次方程的两个根,计算出
的一元二次方程的两个根,计算出![]() ,
,![]() ,计算
,计算![]() ,根据根与系数关系,化简
,根据根与系数关系,化简![]() ,最后计算出
,最后计算出![]() =0,这样就证明出以
=0,这样就证明出以![]() 为直径的圆恒过点M.
为直径的圆恒过点M.
解:(1)解:当![]() 的坐标为
的坐标为![]() 时,设过
时,设过![]() 点的切线方程为
点的切线方程为![]() ,
,
由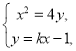 消
消![]() 得
得![]() . (1)
. (1)
令![]() ,解得
,解得![]() .
.
代入方程(1),解得A(2,1),B(-2,1).
设圆心![]() 的坐标为
的坐标为![]() ,由
,由![]() ,得
,得![]() ,解得
,解得![]() .
.
故过![]() 三点的圆的方程为
三点的圆的方程为![]() .
.
(2)证明:设![]() ,由已知得
,由已知得![]() ,
,![]() ,设切点分别为
,设切点分别为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
切线![]() 的方程为
的方程为![]() 即
即![]() ,
,
切线![]() 的方程为
的方程为![]() 即
即![]() .
.
又因为切线![]() 过点
过点![]() ,所以得
,所以得![]() . ①
. ①
又因为切线![]() 也过点
也过点![]() ,所以得
,所以得![]() . ②
. ②
所以![]() ,
,![]() 是方程
是方程![]() 的两实根,
的两实根,
由韦达定理得![]()
![]() .
.
因为![]() ,
,![]() ,
,
所以![]()
![]() .
.
将![]()
![]() 代入,得
代入,得![]() .
.
所以以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .
.

【题目】为了了解校园噪音情况,学校环保协会对校园噪音值(单位:分贝)进行了![]() 天的监测,得到如下统计表:
天的监测,得到如下统计表:
噪音值(单位:分贝) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据该统计表,求这![]() 天校园噪音值的样本平均数(同一组的数据用该组组间的中点值作代表).
天校园噪音值的样本平均数(同一组的数据用该组组间的中点值作代表).
(2)根据国家声环境质量标准:“环境噪音值超过![]() 分贝,视为重度噪音污染;环境噪音值不超过
分贝,视为重度噪音污染;环境噪音值不超过![]() 分贝,视为度噪音污染.”如果把由上述统计表算得的频率视作概率,回答下列问题:
分贝,视为度噪音污染.”如果把由上述统计表算得的频率视作概率,回答下列问题:
(i)求周一到周五的五天中恰有两天校园出现重度噪音污染而其余三天都是轻度噪音污染的概率.
(ii)学校要举行为期![]() 天的“汉字听写大赛”校园选拔赛,把这
天的“汉字听写大赛”校园选拔赛,把这![]() 天校园出现的重度噪音污染天数记为
天校园出现的重度噪音污染天数记为![]() ,求
,求![]() 的分布列和方差
的分布列和方差![]() .
.
【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表,经过进一步统计分析,发现y与x具有线性相关关系.
价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(1)根据上表给出的数据,求出y与x的线性回归方程![]() ;
;
(2)利用(1)中的回归方程,当价格![]() 元/kg时,日需求量y的预测值为多少?
元/kg时,日需求量y的预测值为多少?
(参考公式:线性回归方程![]() ,其中
,其中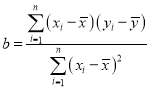 ,
,![]() .)
.)