Question

【题目】在正四棱锥P﹣ABCD中，PA= AB，M是BC的中点，G是△PAD的重心，则在平面PAD中经过G点且与直线PM垂直的直线有条．

Answer 1

【答案】无数
【解析】设正四棱锥的底面边长为a，则侧棱长为 a．
由PM⊥BC，
∴PM= a．
连接PG并延长与AD相交于N点
则PN= a，MN=AB=a，
∴PM2+PN2=MN2 ，
∴PM⊥PN，又PM⊥AD，
∴PM⊥面PAD，
∴在平面PAD中经过G点的任意一条直线都与PM垂直．
所以答案是无数．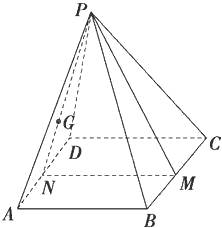

【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点，需要掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题．