题目内容
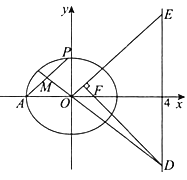
【题目】已知椭圆![]() :
: ![]() (
(![]() )过点
)过点![]() ,且椭圆
,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,且
两点,且![]() 为线段
为线段![]() 中点,再过
中点,再过![]() 作直线
作直线![]() .求直线
.求直线![]() 是否恒过定点,如果是则求出该定点的坐标,不是请说明理由。
是否恒过定点,如果是则求出该定点的坐标,不是请说明理由。
【答案】(1)![]() ;(2)直线
;(2)直线![]() 恒过定点
恒过定点![]() .
.
【解析】试题分析:本题主要考查椭圆的标准方程以及几何性质、直线的标准方程、直线与椭圆的位置关系、韦达定理等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用点在椭圆上和离心率得到方程组,解出a和b的值,从而得到椭圆的标准方程;第二问,需要对直线MN的斜率是否存在进行讨论,(ⅰ)若存在点P在MN上,设出直线MN的方程,由于直线MN与椭圆相交,所以两方程联立,得到两根之和,结合中点坐标公式,得到直线MN的斜率,由于直线MN与直线![]() 垂直,从而得到直线
垂直,从而得到直线![]() 的斜率,因为直线
的斜率,因为直线![]() 也过点P,写出直线
也过点P,写出直线![]() 的方程,经过整理,即可求出定点,(ⅱ)若直线MN的斜率不存在,则直线MN即为
的方程,经过整理,即可求出定点,(ⅱ)若直线MN的斜率不存在,则直线MN即为![]() ,而直线
,而直线![]() 为x轴,经验证直线
为x轴,经验证直线![]() ,也过上述定点,所以综上所述,有定点.
,也过上述定点,所以综上所述,有定点.
(1)因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() , 所以
, 所以![]() , 1分
, 1分
因为椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,即
,即![]() , 2分
, 2分
解得![]() , 所以椭圆
, 所以椭圆![]() 的方程为
的方程为![]() . 4分
. 4分
(2)设![]() ,
, ![]() ,
,
①当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,
,
由 得
得![]() ,
,
所以![]() , 因为
, 因为![]() 为
为![]() 中点,所以
中点,所以![]() ,即
,即![]() .
.
所以![]() , 8分
, 8分
因为直线![]() ,所以
,所以![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
即![]() ,显然直线
,显然直线![]() 恒过定点
恒过定点![]() . 10分
. 10分
②当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,此时直线
,此时直线![]() 为
为![]() 轴,也过点
轴,也过点![]() .
.
综上所述直线![]() 恒过定点
恒过定点![]() . 12分
. 12分

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目