Question

【题目】三棱锥P﹣ABC的高为PH，若三个侧面两两垂直，则H为△ABC的（ ）
A.内心
B.外心
C.垂心
D.重心

Answer 1

【答案】C
【解析】解答：如图所示，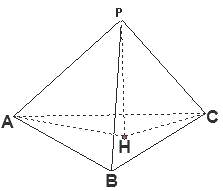
三个侧面两两垂直，可看成正方体的一角，则AP⊥面PBC，
而BC平面PBC∴AP⊥BC而PH⊥面ABC，BC面ABC
∴PH⊥BC，又AP∩PH=P，
∴BC⊥面APH，而AH面APH
∴AH⊥BC，同理可得CH⊥AB
故H为△ABC的垂心
故选：C
分析：先画出图形，三个侧面两两垂直，可看成正方体的一角，根据BC⊥面APH，而AH面APH，推出AH⊥BC，同理可推出CH⊥AB，得到H为△ABC的垂心．
【考点精析】根据题目的已知条件，利用平面与平面垂直的性质的相关知识可以得到问题的答案，需要掌握两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．