题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C. 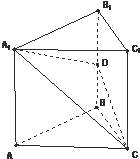
(1)求证:D点为棱BB1的中点;
(2)判断四棱锥A1﹣B1C1CD和C﹣A1ABD的体积是否相等,并证明.
【答案】
(1)过点D作DE⊥A1C于E点,取AC的中点F,连BF,EF.
∵面DA1C⊥面AA1C1C且相交于A1C,面DA1C内的直线DE⊥A1C,
∴DE⊥面AA1C1C.
又∵面BAC⊥面AA1C1C且相交于AC,且△ABC为等腰三角形,易知BF⊥AC,
∴BF⊥面AA1C1C.由此知:DE∥BF,从而有D,E,F,B共面,又易知BB1∥面AA1C1C,
故有DB∥EF,从而有EF∥AA1,又点F是AC的中点,
所以 ,所以D点为棱BB1的中点.
(2)相等.证明:ABC﹣A1B1C1为直三棱柱,
∴BB1⊥A1B1,BB1⊥BC,
又A1B1⊥B1C1,BC⊥AB,
∴A1B1⊥平面B1C1CD,BC⊥平面A1ABD(9分)
∴
∵D为BB1中点,
∴ =
【解析】分析:(1)过点D作DE⊥A1C于E点,取AC的中点F,连BF,EF,推出 ![]() ,即可证明D点为棱BB1的中点;(2)求出四棱锥A1﹣B1C1CD的底面面积和高,再计算C﹣A1ABD的体积,即可判断体积相等.
,即可证明D点为棱BB1的中点;(2)求出四棱锥A1﹣B1C1CD的底面面积和高,再计算C﹣A1ABD的体积,即可判断体积相等.
【考点精析】掌握平面与平面垂直的性质是解答本题的根本,需要知道两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.

【题目】某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
年份200x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十)万 | 5 | 7 | 8 | 11 | 19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出Y关于x的线性回归方程Y=bx+a;
(3)据此估计2005年该城市人口总数.