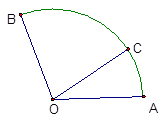
题目内容
(本题满分12分)
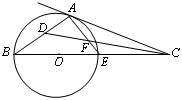
如图,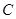 点在圆
点在圆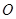 直径
直径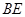 的延长线上,
的延长线上,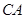 切圆
切圆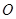 于
于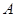 点,
点,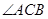 的平分线
的平分线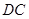 交
交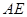 于点
于点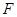 ,交
,交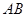 于
于 点.
点.
(I)求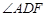 的度数;
的度数;
(II)当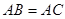 时,求证:
时,求证: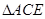 ∽
∽ ,并求相似比
,并求相似比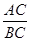 的值.
的值.
如图,
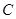 点在圆
点在圆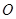 直径
直径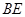 的延长线上,
的延长线上,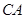 切圆
切圆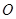 于
于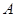 点,
点,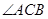 的平分线
的平分线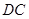 交
交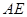 于点
于点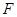 ,交
,交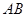 于
于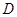 点.
点.
(I)求
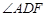 的度数;
的度数;(II)当
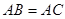 时,求证:
时,求证: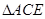 ∽
∽ ,并求相似比
,并求相似比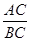 的值.
的值.(I)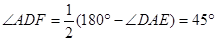 ;(II)
;(II)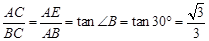 。
。
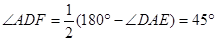 ;(II)
;(II)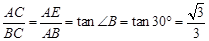 。
。本试题主要是考查了平面几何中圆内的性质和三角形的相似的性质的综合运用。
(1)根据已知AC为圆O的切线,利用弦切角定理和角平分线的性质得到角相等,进而确定结论。
(2)根据第一问中角的关系,然后结合三角形ACE相似于三角形ABC,可知结论。
(I)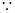 AC为圆O的切线,∴
AC为圆O的切线,∴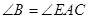
又知DC是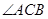 的平分线, ∴
的平分线, ∴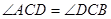 ……………………………………3分
……………………………………3分
∴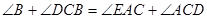 即
即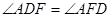 又因为BE为圆O的直径,
又因为BE为圆O的直径,
∴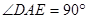 ∴
∴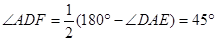 ……………………………………….6分
……………………………………….6分
(II)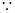
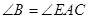 ,
,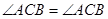 ,∴
,∴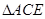 ∽
∽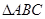 ……….………8分
……….………8分
∴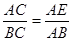 ,又
,又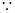 AB="AC," ∴
AB="AC," ∴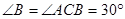 , ………10分
, ………10分
∴在RT△ABE中,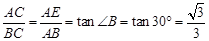 ……………………………………….12分
……………………………………….12分
(1)根据已知AC为圆O的切线,利用弦切角定理和角平分线的性质得到角相等,进而确定结论。
(2)根据第一问中角的关系,然后结合三角形ACE相似于三角形ABC,可知结论。
(I)
 AC为圆O的切线,∴
AC为圆O的切线,∴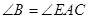
又知DC是
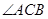 的平分线, ∴
的平分线, ∴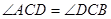 ……………………………………3分
……………………………………3分∴
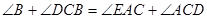 即
即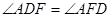 又因为BE为圆O的直径,
又因为BE为圆O的直径, ∴
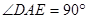 ∴
∴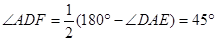 ……………………………………….6分
……………………………………….6分(II)
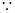
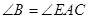 ,
,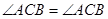 ,∴
,∴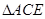 ∽
∽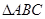 ……….………8分
……….………8分∴
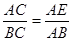 ,又
,又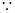 AB="AC," ∴
AB="AC," ∴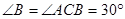 , ………10分
, ………10分∴在RT△ABE中,
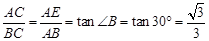 ……………………………………….12分
……………………………………….12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
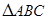 中,
中,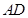 为
为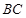 边上的中线,
边上的中线,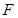 为
为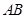 上任意一点,
上任意一点,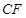 交
交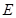 .求证:
.求证: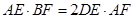 .
. 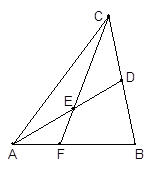
 上一点
上一点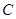 在直径
在直径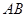 上的射影为
上的射影为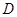 .
.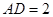 ,
,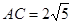 ,则
,则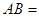 .
.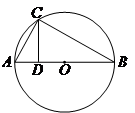
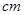 和18
和18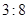 ,则另一弦的
,则另一弦的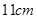
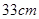
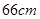
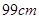
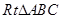 的直角边
的直角边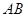 为直径作圆
为直径作圆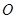 ,圆
,圆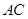 交于
交于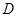 ,过
,过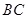 交于
交于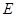 ,若
,若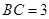 ,
,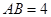 ,则
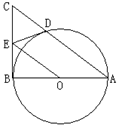
,则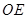 ="_________"
="_________" 
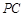 切⊙
切⊙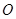 于点
于点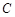 ,割线
,割线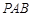 经过圆心
经过圆心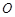 ,弦
,弦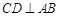 于点
于点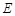 .已知⊙
.已知⊙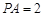 ,则
,则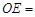 .
.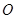 外一点
外一点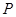 引圆的一条切线
引圆的一条切线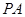 ,切点为
,切点为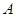 ,
,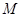 为
为 两点,且
两点,且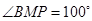 ,
,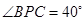 .
.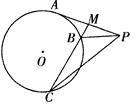
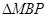 与
与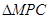 相似;
相似;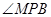 的大小.
的大小.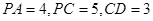 ,则
,则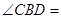 ( )
( )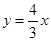 ;③y=2;④y=2x+1.
;③y=2;④y=2x+1.