题目内容
【题目】一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为V1 ， V2 ， V3 ， V4 ， 上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则有（ ）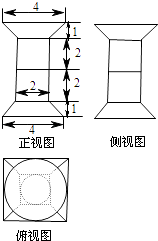 
A.V1＜V2＜V4＜V3
B.V1＜V3＜V2＜V4
C.V2＜V1＜V3＜V4
D.V2＜V3＜V1＜V4
【答案】C
【解析】解：由题意以及三视图可知，该几何体从上到下由：圆台、圆柱、正四棱柱、正四棱台组成，
体积分别记为V1= 
= 
．
V2=12×π×2=2π，
V3=2×2×2=8
V4= 
= 
；
∵ 
，
∴V2＜V1＜V3＜V4
故选C．
【考点精析】解答此题的关键在于理解由三视图求面积、体积的相关知识，掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
【题目】已知变量
之间的线性回归方程为
，且变量之间的一组相关数据如表所示，则下列说法错误的是（ ）
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量之间呈现负相关关系
B. 
的值等于5
C. 变量之间的相关系数
D. 由表格数据知，该回归直线必过点（9，4）
