题目内容

7．已知棱长为1的正方体ABCD-A1B1C1D1中，E、F分别是AB、AD的中点，点P，Q分别在棱A1B1、A1D1上，且A1P=A1Q=x（0＜x＜1），设平面MEF∩平面MPQ=l，则下列结论中错误的是（　　）
A．l∥平面ABCD
B．l⊥AC
C．存在x0∈（0，1），使平面MEF与平面MPQ垂直
D．当x变化时，l是定直线

分析 画出直线l，然后判断选项即可．根据空间线面关系的判定方法，逐一分析四个答案的真假，可得结论．

解答 解：如图作出过M的中截面，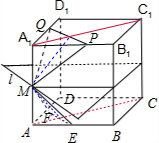

∵棱长为1的正方体ABCD-A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，
又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，
∵QP∥EF，EF∥中截面，由平面与平面平行的性质定理，可知：面MEF∩面MPQ=l，
由平面与平面平行的性质定理可知：l∥面ABCD，故A结论正确；
∵几何体是正方体，
∴AC⊥EF，由三垂线定理可知：l⊥AC，故B结论正确．
过ACC1A1的平面如图，图中两条蓝色射线的夹角，即为平面MEF与平面MPQ所成二面角的平面角，
则当Q、P与D1，B1重合时，面MEF与面MPQ垂直，此时x0=1∉（0，1），故C结论错误；
直线l与EF平行，是定直线．故D结论正确．
故选：C．

点评 本题考查空间想象能力，直线与平面，直线与直线的位置关系，考查逻辑推理能力．

练习册系列答案
相关题目
17．某医疗研究所为了检验某种血清预防感冒的作用，把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较，提出假设H0：“这种血清不能起到预防感冒的作用”，利用2×2列联表计算的结果，认为H0成立的可能性不足1%，那么K2的一个可能取值为（　　）参考数据
P（K2≥k0）     0.05 0.025 0.010 0.005 0.001
 k0 3.841 5.024 6.635 7.879 10.83
A．6.635B．7.897C．5.024D．3.841
18．函数f（x）的部分图象如图所示，则f（x）的解析式可以是（　　）
A．f（x）=x+sinxB．f（x）=x•sinxC．f（x）=x•cosxD．f（x）=x（x-$\frac{π}{2}$）（x-$\frac{3π}{2}$）
15．在平面直角坐标系xOy中，E，F两点的坐标分别为（0，1）、（0，-1），动点G满足：直线EG与直线FG的斜率之积为$-\frac{1}{4}$．
（1）求动点G的轨迹方程；
（2）设A，B为动点G的轨迹的左右顶点，P为直线l：x=4上的一动点（点P不在x轴上），连AP交G的轨迹于C点，连PB并延长交G的轨迹于D点，试问直线CD是否过定点？若成立，请求出该定点坐标，若不成立，请说明理由．
2．已知数列{an}是公比为$\frac{1}{2}$的等比数列，数列{bn}满足a1=$\sqrt{2}$b1=1，且an+12=$\frac{（{a}_{n}+{b}_{n}）^{2}}{{{a}_{n}}^{2}+{{b}_{n}}^{2}}$，bn+1=1+$\frac{{b}_{n}}{{a}_{n}}$，n∈N+，若cn=$\frac{{{b}_{n}}^{2}}{{{a}_{n}}^{2}}$；
（1）求证：数列{cn}是等差数列，并求出{cn}的通项公式；
（2）记数列{cn}的前n项和为Sn，若对于?n∈N+，不等式$\sum_{i=1}^{n}$ai$\sqrt{{S}_{i}}$≤k-$\frac{\sqrt{2}n}{{2}^{n}}$恒成立，求实数k的取值范围．
12．如图，在圆锥PO中，已知PO=$\sqrt{2}$，⊙O的直径AB=2，AB上的点C平分该弧．
（1）证明：平面POD⊥平面PAC；
（2）求二面角B-PA-C的余弦值．
19．有4名优秀学生A，B，C，D全部被保送到甲，乙，丙3所学校，每所学校至少去一名，则不同的保送方案共有（　　）
A．26种B．32种C．36种D．56种
16．已知全集U=R，若集合A={y|y=3-2-x}，B={x|x=$\frac{x-2}{x}$≤0}，则A∩（CUB）=（　　）
A．（-∞，0）∪[2，3）B．（-∞，0]∪（2，3）C．[0.2）D．[0.3）
13．已知数列{an}的通项公式an=|3n-$\frac{k}{{3}^{n}}$|，若{an}为单调递增数列，则实数k的取值范围是（-27，27）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网