题目内容
3.在△ABC中,三内角A,B,C的对边分别为a,b,c且a2=b2+c2+bc,a=$\sqrt{3}$,S为△ABC的面积,则S+$\sqrt{3}$cosBcosC的最大值为( )| A. | 1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{3}$ | D. | 3 |
分析 运用余弦定理可得A,再由正弦定理可得外接圆的半径,再由三角形的面积公式和两角差的余弦公式,结合余弦函数的值域,即可得到最大值.
解答 解:∵a2=b2+c2+bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{-bc}{2bc}$=-$\frac{1}{2}$,
由0<A<π,可得A=$\frac{2π}{3}$,
设△ABC外接圆的半径为R,则2R=$\frac{a}{sinA}$=$\frac{\sqrt{3}}{sin\frac{2π}{3}}$=2,
解得R=1,
∴S+$\sqrt{3}$cosBcosC=$\frac{1}{2}$bcsinA+$\sqrt{3}$cosBcosC=$\frac{\sqrt{3}}{4}$bc+$\sqrt{3}$cosBcosC
=$\sqrt{3}$sinBsinC+$\sqrt{3}$cosBcosC=$\sqrt{3}$cos(B-C),
故S+$\sqrt{3}$cosBcosC的最大值为$\sqrt{3}$.
故选C.
点评 本题考查正弦定理和余弦定理和三角形的面积公式的运用,同时考查两角和差的余弦公式和余弦函数的值域,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
13.两球O1和O2在棱长为1的正方体ABCD-A1B1C1D1的内部,且互相外切,若球O1与过点A的正方体的三个面相切,球O2与过点C1的正方体的三个面相切,则球O1和O2的表面积之和的最小值为( )
| A. | 3(2-$\sqrt{3}$)π | B. | 4(2-$\sqrt{3}$)π | C. | 3(2+$\sqrt{3}$)π | D. | 4(2+$\sqrt{3}$)π |
14.设全集U=R,集合M={x|0<x≤1},N={x|x≤0},则M∩(∁UN)=( )
| A. | {x|0≤x<1} | B. | {x|0<x≤1} | C. | {x|0≤x≤1} | D. | {x|x<1} |
18.函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )
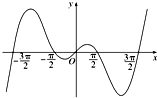

| A. | f(x)=x+sinx | B. | f(x)=x•sinx | C. | f(x)=x•cosx | D. | f(x)=x(x-$\frac{π}{2}$)(x-$\frac{3π}{2}$) |
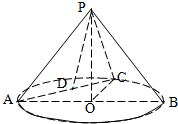 如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,AB上的点C平分该弧.
如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,AB上的点C平分该弧.