题目内容
【题目】已知正整数![]() 满足
满足![]() ,
,![]() .令
.令![]() ,
, ![]() ,
, ![]() .对任意的
.对任意的![]() ,记
,记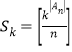 ,其中,
,其中,![]() 表示不超过实数
表示不超过实数![]() 的最大整数,
的最大整数,![]() 表示集合
表示集合![]() 中元素的个数.证明:
中元素的个数.证明:
(1)![]() ;
;
(2)![]() .
.
【答案】(1)见解析(2)见解析
【解析】
显然,![]() 为奇数,
为奇数,![]() 为偶数,其中,
为偶数,其中,![]() 为欧拉函数.
为欧拉函数.
由欧拉定理,知对任意的![]() ,有
,有![]()
于是,对集合![]() 的任意子集
的任意子集![]() 有
有
![]()
![]()
![]()
![]() .①
.①
首先证明:![]() ,且均为奇数.
,且均为奇数.
由![]() ,知集合
,知集合![]() 在数轴上关于点
在数轴上关于点![]() 对称,且
对称,且![]() 、
、![]() .
.
将集合![]() 中连续的正整数称为一段,则由
中连续的正整数称为一段,则由![]() 的对称性知其可分成奇数段,每段中均有一个数属于集合
的对称性知其可分成奇数段,每段中均有一个数属于集合![]() ,也有一个数属于集合
,也有一个数属于集合![]() .
.
则![]() 为奇数,且集合
为奇数,且集合![]() 与
与![]() 关于
关于![]() 对称,即
对称,即![]() .
.
故 .
.
其次证明:对任意的![]() ,存在唯一的
,存在唯一的![]() ,使得
,使得![]() .
.
考虑![]() .
.
显然,![]() .
.
若![]() ,则
,则![]() ,矛盾.
,矛盾.
故![]() 模
模![]() 两两不同余,其中恰有一个数模
两两不同余,其中恰有一个数模![]() 余1.
余1.
又![]() ,故集合
,故集合![]() 中其余数可两两配对,每对的积模
中其余数可两两配对,每对的积模![]() 余1.
余1.
从而,![]() .
.
取![]() ,则
,则![]() ,且
,且![]() ,
,![]() .
.
再证明:![]() 中的数可两两配对,每对数的积模
中的数可两两配对,每对数的积模![]() 余1.即证明:对任意的
余1.即证明:对任意的![]()
![]() ,则
,则![]() .
.
否则,不妨设![]() ,即
,即![]() 、
、![]() ,
,![]() ,
,![]() .
.
设![]() .则
.则
![]() ,这与
,这与![]() 矛盾.
矛盾.
从而,![]() .
.
最后,在式①中令![]() 得
得
 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目