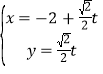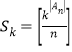题目内容
【题目】设
，
为三维空间中
个点组成的有限集，其中任意四点不在一个平面上，将集合中的点染成白色或黑色，使得任意一个与集合至少交于四个点的球面具有这样的性质：这些交点中恰有一半的点为白色的.证明：集合中所有的点均在一个球面上，
【答案】见解析
【解析】
定义
：
为
由已知条件，知
，其中，
表示至少经过集合
的四个点的任一球面.
对于集合中任意的三个不同的点
、
、
，
用
表示经过点、、且还至少经过集合中的另一个点的所有球面组成的集合，
表示这些球面的个数.
故
.①
这是因为、、的值出现次，而其他的值只出现一次.
若存在三个点使得
，则结论得证.
若对集合M中任意的三个不同的点、、，
，先证明
.
假设
.则由式①知
，所有的
的组合共有
种.
对所有的这些可能求和有
，这与假设矛盾.
同理，若
，也会推出矛盾.
接下来，由及式①，得出对集合中任意的三个不同的点、、，有
.
取另一个点
，得到下列等式：
，
，
，
.
由此，容易推出
，这与的定义矛盾.
练习册系列答案
相关题目
