Question

【题目】已知中心在原点的双曲线的右焦点为，右顶点为．

（）求双曲线的方程；

（）若直线与双曲线交于不同的两点，，且线段的垂直平分线过点，求实数的取值范围．

Answer 1

【答案】（1）；（2）.

【解析】试题分析：（1）由双曲线的右焦点为，右顶点为求出和,进而根据求得,则双曲线方程可得；（2）把直线方程与双曲线方程联立，消去，利用判别式大于求得和的不等式关系，设的中点为，根据韦达定理表示出和，根据，可知的斜率为，进而求得和的关系，最后综合可求得的范围.

试题解析：（）设双曲线方程为．

由已知得，，，

∴．

故双曲线的方程为．

（）联立，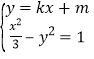

整理得．

∵直线与双曲线有两个不同的交点，

∴，

可得．（）

设、，的中点为．

则，，．

由题意，，∴．

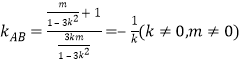整理得．（）

将（）代入（），得，

∴或．

又，即．

∴的取值范围是．

【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系，属于难题. 用待定系数法求椭圆方程的一般步骤；①作判断：根据条件判断椭圆的焦点在轴上，还是在轴上，还是两个坐标轴都有可能；②设方程：根据上述判断设方程或 ；③找关系：根据已知条件，建立关于、、的方程组；④得方程：解方程组，将解代入所设方程，即为所求.