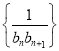题目内容
【题目】设公差不为零的等差数列{an}的前5项的和为55，且a2 ， 
﹣9成等比数列．
（1）求数列{an}的通项公式．
（2）设数列bn= 
，求证：数列{bn}的前n项和Sn＜ 
．
【答案】
（1）解：设等差数列的首项为a1，公差为d，
由题意可得 
，
即有 
或 
（舍去），
故数列{an}的通项公式为an=7+2（n﹣1）即an=2n+5
（2）证明：由（1）an=2n+5，
得 
，
则 
= 
．
故原不等式成立
【解析】（1）设等差数列的首项为a1 ， 公差为d，运用等比数列的中项的性质和等差数列的通项公式和求和公式，解方程可得首项和公差，即可得到所求通项公式；（2）求得bn= 
（ 
﹣ 
），运用裂项相消求和和不等式的性质，即可得证．
练习册系列答案
名校课堂系列答案
相关题目
