题目内容
9.已知函数f(x)=|x-2|-|x-5|.(1)求函数f(x)的值域;
(2)设a,b∈{y|y=f(x)},试比较3|a+b|与|ab+9|的大小.
分析 (1)利用绝对值的性质,可得∴||x-2|-|x-5||≤=|x-2-(x-5)|=3,进而求出函数f(x)的值域;
(2)由a,b∈[-3,3],可得-9≤ab≤9,即ab+9≥0,分a+b≥0时和a+b<0时两种情况,分析|ab+9|-3|a+b|的符号,可得结论.
解答 解:(1)∵函数f(x)=|x-2|-|x-5|.
∴||x-2|-|x-5||≤=|x-2-(x-5)|=3,
故-3≤|x-2|-|x-5|≤3,
即函数f(x)的值域为[-3,3],
(2)∵a,b∈{y|y=f(x)},
∴a,b∈[-3,3],
则-9≤ab≤9,则ab+9≥0,|ab+9|=ab+9,
当a+b≥0时,|ab+9|-3|a+b|=ab+9-3a-3b=(a-3)(b-3)≥0,此时3|a+b|≤|ab+9|,
当a+b<0时,|ab+9|-3|a+b|=ab+9+3a+3b=(a+3)(b+3)≥0,此时3|a+b|≤|ab+9|,
综上3|a+b|≤|ab+9|.
点评 本题考查的知识点是绝对值函数,作差法比较大小,是绝对值函数与不等式证明的综合应用,难度中档.

练习册系列答案
相关题目
19.设函数f(x)是定义在R上的奇函数,且对任意x∈R都有f(x)=f(x+4),当x∈(0,2)时,f(x)=2x,则f(2015)+f(2012)的值为( )
| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
17.给出下列实际问题:①一种药物对某种病的治愈率;②两种药物冶疗同一种病是否有区别;③吸烟者得肺病的概率;④吸烟人群是否与性别有关系;⑤网吧与青少年的犯罪是否有关系.其中,用独立性检验可以解决的问题有( )
| A. | ①②③ | B. | ②④⑤ | C. | ②③④⑤ | D. | ①②③④⑤ |
4.设全集U=R,集合R={0,1,2},B={x|$\frac{1}{x-1}$>0,x∈R},则A∩∁UB=( )
| A. | {0} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
18.一条渔船以6km/h的速度向垂直于对岸的方向行驶,同时河水的流速为2km/h,则这条渔船实际航行的速度大小为( )
| A. | $2\sqrt{10}$km/h | B. | $4\sqrt{2}$km/h | C. | 2$\sqrt{3}$km/h | D. | 3km/h |
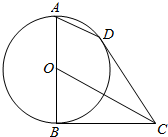 如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.
如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.