题目内容
【题目】甲、乙两位同学分别做下面这道题目：在平面直角坐标系中，动点
到
的距离比到
轴的距离大
，求的轨迹.甲同学的解法是：解：设的坐标是
，则根据题意可知
，化简得
； ①当
时，方程可变为
；②这表示的是端点在原点、方向为
轴正方向的射线，且不包括原点； ③当
时，方程可变为
； ④这表示以为焦点，以直线
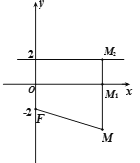
为准线的抛物线；⑤所以的轨迹为端点在原点、方向为轴正方向的射线，且不包括原点和以为焦点，以直线为准线的抛物线. 乙同学的解法是：解：因为动点到的距离比到轴的距离大. ①如图，过点
作轴的垂线，垂足为
. 则
.设直线
与直线的交点为
，则
； ②即动点到直线的距离比到轴的距离大； ③所以动点到的距离与到直线的距离相等；④所以动点的轨迹是以为焦点，以直线为准线的抛物线； ⑤甲、乙两位同学中解答错误的是________（填“甲”或者“乙”），他的解答过程是从_____处开始出错的（请在横线上填写① 、②、③、④ 或⑤ ）.
【答案】乙 ②
【解析】
由题干
的坐标是
可以是平面直角坐标系中的任意一点，根据甲、乙的解题过程即可求解.
由在平面直角坐标系中，动点到
的距离比到
轴的距离大
，
可得
，讨论
的正负，整理化简，故甲正确；
对于乙，由于在轴上方也存在满足条件的点，乙选择点具有特殊性，从②即动点到直线
的距离比到轴的距离大；把点定为在轴下方，故从②开始错误；
故答案为：乙；②
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
