题目内容
【题目】已知关于![]() 的不等式
的不等式![]() 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数
有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
【答案】D
【解析】
化简不等式可得mex<![]() ,根据两函数的单调性得出正整数解为1和2,列出不等式组解出即可.
,根据两函数的单调性得出正整数解为1和2,列出不等式组解出即可.
当x>0时,由x2﹣mxex﹣mex>0,可得mex<![]() (x>0),
(x>0),
显然当m≤0时,不等式mex<![]() (x>0),在(0,+∞)恒成立,不符合题意;
(x>0),在(0,+∞)恒成立,不符合题意;
当m>0时,令f(x)=mex,则f(x)在(0,+∞)上单调递增,
令g(x)=![]() ,则g′(x)=
,则g′(x)=![]() =
=![]() >0,
>0,
∴g(x)在(0,+∞)上单调递增,
∵f(0)=m>0,g(0)=0,且f(x)<g(x)有两个正整数解,
则∴ ,即
,即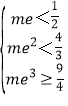 ,解得
,解得![]() ≤m<
≤m<![]() .
.
故选:D.

练习册系列答案
相关题目