题目内容
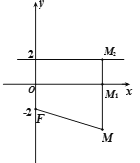
【题目】已知圆
与圆
.
（1）若圆
与圆
外切，求实数m的值；
（2）在（1）的条件下，若直线l与圆的相交弦长为
且过点
，求直线l的方程.
【答案】（1）
；（2）直线l方程为：
或
【解析】
（1）先根据圆的方程求出圆心坐标和半径，再由由圆
与圆
外切，可知两圆心的距离等于两圆半径之和，代入数据求解即可；
（2）分析可知弦的垂直平分线过圆心，由勾股定理可求出圆心到直线的距离，再由直线l过点
，可设出直线方程，分斜率存在和不存在两种情况，求出方程即可.
（1）
，
，
，
，
，
，
圆与圆外切，
，
，
；
（2）由（1）得，圆的方程为
，
设圆心到直线l的距离
，因为直线l与圆的相交弦长为
，则有
，代入数据解得
，
当直线l无斜率时：直线方程为.符合题意.
当直线l斜率为k时，则直线方程为
，
化为一般形式为
，
则圆心
到直线l的距离
，解得
.
综上，直线l方程为：或.
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
