题目内容
【题目】某海湿地如图所示,A、B和C、D分别是以点O为中心在东西方向和南北方向设置的四个观测点,它们到点O的距离均为![]() 公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
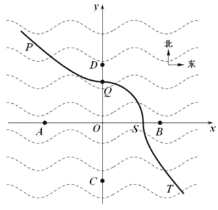
(1)求观光长廊PQST所在的曲线的方程;
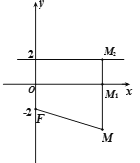
(2)在观光长廊的PQ段上,需建一服务站M,使其到观测点A的距离最近,问如何设置服务站M的位置?
【答案】(1)![]()
(2)![]()
【解析】
(1)由题意知,QS的轨迹为圆的一部分,PQ的轨迹为双曲线的一部分,ST的轨迹为双曲线的一部分,分别求出对应的轨迹方程即可;
(2)由题意设点M(x,y),计算|MA|2的解析式,再求|MA|的最小值与对应的x、y的值.
解:(1)①由题意知,QS段上的任意一点到中心点O的距离都相等,
QS的轨迹为圆的一部分,其中r=4,圆心坐标为O,
即x≥0、y≥0时,圆的方程为x2+y2=16;
②PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,
PQ的轨迹为双曲线的一部分,且c=4![]() ,a=4,
,a=4,
即x<0、y>0时,双曲线方程为![]() 1;
1;
③ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,
ST的轨迹为双曲线的一部分,且c=4![]() ,a=4,
,a=4,
即x>0、y<0时,双曲线方程为![]() 1;
1;
综上,x≥0、y≥0时,曲线方程为x2+y2=16;
x<0、y>0时,曲线方程为![]() 1;
1;
x>0、y<0时,曲线方程为![]() 1;
1;
[注]可合并为![]() 1;
1;
(2)由题意设点M(x,y),其中![]() 1,其中x≤0,y≥0;
1,其中x≤0,y≥0;
则|MA|2![]() y2
y2![]() x2+16=2
x2+16=2![]() 32;
32;
当且仅当x=﹣2![]() 时,|MA|取得最小值为
时,|MA|取得最小值为![]() 4
4![]() ;
;
此时y=4![]() 2
2![]() ;
;
∴点M(﹣2![]() ,2
,2![]() ).
).

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案