题目内容
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 与直线
与直线![]() 平行,且过坐标原点,圆
平行,且过坐标原点,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 和圆
和圆![]() 相交于点
相交于点![]() 、
、![]() 两点,求
两点,求![]() 的周长.
的周长.
【答案】(1)直线![]() 的极坐标方程为
的极坐标方程为![]() 。圆C的极方程为
。圆C的极方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)先将直线和圆的参数方程化为普通方程,进而可得其极坐标方程;
(2)将直线的极坐标方程代入圆的极坐标方程,可求出关于![]() 的方程,由
的方程,由![]() ,即可求出结果.
,即可求出结果.
(I)因为直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),所以直线
为参数),所以直线![]() 的斜率为1,因为直线
的斜率为1,因为直线![]() 与直线
与直线![]() 平行,且过坐标原点,所以直线
平行,且过坐标原点,所以直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,所以直线
,所以直线![]() 的极坐标方程为
的极坐标方程为![]()
因为圆C的参数方程为![]() (
(![]() 为参数),
为参数),
所以圆C的普通方程为![]() ,
,
即![]() ,
,
所以圆C的极方程为![]()
(Ⅱ)把直线m的极坐标方程![]() 代入
代入![]() 中得,
中得,
![]() ,
,
所以![]()
所以△ABC的周长为![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.

组别 | 分组 | 回答正确的人数 | 回答正确的人数占本组的概率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) |
| 0.9 |
第3组 | [35,45) | 27 |
|
第4组 | [45,55) |
| 0.36 |
第5组 | [55,65) | 3 |
|
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
【题目】大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程.
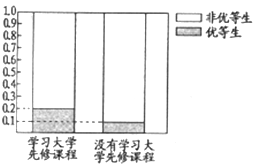
(Ⅰ)这两年学校共培养出优等生150人,根据下图等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 250 | ||
没有学习大学先修课程 | |||
总计 | 150 |
(Ⅱ)某班有5名优等生,其中有2名参加了大学生先修课程的学习,在这5名优等生中任选3人进行测试,求这3人中至少有1名参加了大学先修课程学习的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]()
【题目】2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取![]() 名学生对线上教学进行调查,其中男生与女生的人数之比为
名学生对线上教学进行调查,其中男生与女生的人数之比为![]() ,抽取的学生中男生有
,抽取的学生中男生有![]() 人对线上教学满意,女生中有
人对线上教学满意,女生中有![]() 名表示对线上教学不满意.
名表示对线上教学不满意.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对线上教学是否满意 与性别有关”;
的把握认为“对线上教学是否满意 与性别有关”;
态度 性别 | 满意 | 不满意 | 合计 |
男生 | |||
女生 | |||
合计 | 100 |
(2)从被调查的对线上教学满意的学生中,利用分层抽样抽取![]() 名学生,再在这
名学生,再在这![]() 名学生中抽取
名学生中抽取![]() 名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
附: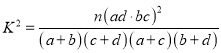 .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |