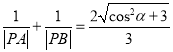题目内容
【题目】已知焦点在x轴上且长轴长为4的椭圆C过点T(1,1),记l为圆O:x2+y2=1的切线
(1)求椭圆C的方程;
(2)若l与椭圆C交于A、B两点,求证:∠AOB为定值.
【答案】(1)![]() =1.(2)见解析.
=1.(2)见解析.
【解析】
(1)利用长轴长和椭圆上的点,构造方程求解出椭圆方程;(2)当直线![]() 斜率不存在时,求得
斜率不存在时,求得![]() 坐标,可求得
坐标,可求得![]() ;当直线
;当直线![]() 斜率存在时,将直线方程与椭圆方程联立,利用韦达定理表示出
斜率存在时,将直线方程与椭圆方程联立,利用韦达定理表示出![]() ,整理化简可得
,整理化简可得![]() ,可得
,可得![]() ;从而可知
;从而可知![]() 为定值
为定值![]() .
.
(1)![]() 焦点在
焦点在![]() 轴上且长轴长为
轴上且长轴长为![]() 的椭圆
的椭圆![]() 过点
过点![]()
![]() 设椭圆方程为
设椭圆方程为![]()
则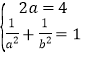 ,解得
,解得![]() ,
,![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
(2)证明:![]() 为圆
为圆![]() 的切线
的切线
![]() 当
当![]() 的斜率不存在时,
的斜率不存在时,![]() 的方程为
的方程为![]()
又![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点
两点
则![]() ,
,![]() 或
或![]() ,
,![]()
![]() ,
,![]() 或
或![]() ,
,![]()
![]()
![]()
![]()
当直线![]() 存在斜率
存在斜率![]() 时,设
时,设![]() 的方程为:
的方程为:![]()
则![]() ,即
,即![]()
联立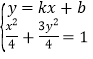 ,得
,得![]()
由题意![]() ,设
,设![]() ,
,![]()
则![]() ,
,![]()
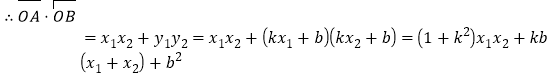
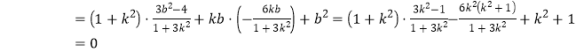
![]()
![]()
![]()
综上可知,![]() 为定值
为定值![]()

 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】治理大气污染刻不容缓,根据我国分布的《环境空气质量数(AQI)技术规定》:空气质量指数划分阶为0~50、51~100、101~150、151~200、201~300和大于300六级,对应于空气质量指数的六个级别,指数越大,级别越高,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数小于![]() 时,可以户外运动;空气质量指数
时,可以户外运动;空气质量指数![]() 及以上,不适合进行旅游等户外活动,以下是某市
及以上,不适合进行旅游等户外活动,以下是某市![]() 年
年![]() 月中旬的空气质量指数情况:
月中旬的空气质量指数情况:
时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
AQI | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
(1)求![]() 月中旬市民不适合进行户外活动的概率;
月中旬市民不适合进行户外活动的概率;
(2)一外地游客在![]() 月中旬来该市旅游,想连续游玩两天,求适合旅游的概率.
月中旬来该市旅游,想连续游玩两天,求适合旅游的概率.
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.

(Ⅰ)以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况,则2018年11月中有多少天的空气质量达到优良?
(Ⅱ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为1000元,空气质量等量等级为3级时每天需净化空气的费用为2000元.若从这10天样本中空气质量为1级、2级、3级的天数中任意抽取两天,求这两天的净化空气总费用为3000元的概率.