题目内容
【题目】若数列![]() 共有k
共有k![]() 项,且同时满足
项,且同时满足![]() ,
,![]() ,则称数列
,则称数列![]() 为
为![]() 数列.
数列.
(1)若等比数列![]() 为
为![]() 数列,求
数列,求![]() 的值;
的值;
(2)已知![]() 为给定的正整数,且
为给定的正整数,且![]() ,
,
①若公差为![]()
![]() 的等差数列
的等差数列![]() 是
是![]() 数列,求公差d;
数列,求公差d;
②若数列![]() 的通项公式为
的通项公式为
![]() ,其中常数
,其中常数![]() ,判断数列
,判断数列![]() 是否为
是否为![]() 数列,并说明理由.
数列,并说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②不是,详见解析
;②不是,详见解析
【解析】
(1)根据新定义结合等比数列即可求出![]() 的值;
的值;
(2)①设等差数列的公差为![]() ,根据新定义以及等差数列的性质即可求出公差
,根据新定义以及等差数列的性质即可求出公差![]() 的值;②若数列
的值;②若数列![]() 是
是![]() 数列,根据新定义,对
数列,根据新定义,对![]() 的值分奇数和偶数两种情况讨论,即可判断出数列
的值分奇数和偶数两种情况讨论,即可判断出数列![]() 是否为
是否为![]() 数列.
数列.
(1)设等比数列的公比为![]() ,
,
∵数列![]() 为
为![]() 数列,∴
数列,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
又∵![]() ,∴
,∴![]() ,解得
,解得![]() ;
;
(2))①设等差数列的公差为![]() ,
,
∵数列![]() 是
是![]() 数列,
数列,
∴![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,且
,且![]() ,
,
∴![]() ,
,
即![]() ,解得
,解得![]() ,
,
∴等差数列![]() 的公差为得
的公差为得![]() ;
;
②若数列![]() 是
是![]() 数列,则有:
数列,则有:![]() ,
,![]() ,
,
∵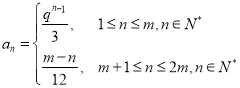 ,且
,且![]() ,
,
∴![]() (*),
(*),
![]() (**),
(**),
当![]() 为偶数时,在(*)中,
为偶数时,在(*)中,![]() ,
,![]() ,所以(*)不成立,
,所以(*)不成立,
当m为奇数时,由(*)+(**)得: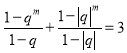 ,
,
又∵![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∵![]() 为奇数,∴
为奇数,∴![]() ,
,
∴![]() ,整理得:
,整理得:![]() ,即
,即![]() ,与
,与![]() 矛盾,
矛盾,
综上可知,数列![]() 不是
不是![]() 数列.
数列.

练习册系列答案
相关题目



