Question

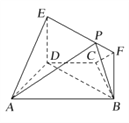
【题目】如图，D是直角△ABC斜边BC上一点，AC= DC．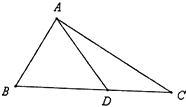
（Ⅰ）若∠DAC=30°，求角B的大小；
（Ⅱ）若BD=2DC，且AD= ，求DC的长．

Answer 1

【答案】解：（Ⅰ）在△ABC中，根据正弦定理，有 = ． ∵AC= DC，∴sin∠ADC= = ．
又∠ADC=∠B+∠BAD=∠B+60°＞60° ，
∴∠ADC=120°．
于是∠C=180°﹣120°﹣30°=30° ， ∴∠B=60°．
（Ⅱ）设DC=x，则BD=2x，BC=3x，AC= x．
于是sinB= = ，cosB= ，AB= x．
在△ABD中，由余弦定理，AD2=AB2+BD2﹣2ABBDcosB，
即 ，得x=1．故DC=1
【解析】（Ⅰ）利用正弦定理、外角性质、三角形内角和定理即可得出．（Ⅱ）设DC=x，则BD=2x，BC=3x，AC= x．于是sinB= = ，cosB= ，AB= x．再利用余弦定理即可得出．