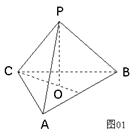
题目内容
如图所示,ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB、PC的中点.求证:MN⊥平面PCD. 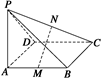

证明略
如图所示,取PD的中点E,连接AE、NE,

∵N、E分别为PC,PD的中点,
∴NE为△PCD的中位线,
∴NE∥CD且NE=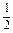 CD.
CD.
又M为AB的中点,
∴AM∥CD且AM=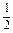 CD,
CD,
∴AM∥NE且AM=NE,
∴四边形AENM为平行四边形,∴AE∥MN.
又△PAD为等腰三角形,∴AE⊥PD,∴MN⊥PD.
连接PM、MC,设AD=a,AB=2b,
∴PM2=a2+b2,CM2=a2+b2,
∴CM=PM,∴MN⊥PC.
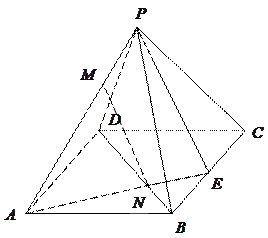
∵PC∩PD=P,∴MN⊥平面PCD.△ABC为正三角形,
D、E分别是BC、CA的中点.

∵N、E分别为PC,PD的中点,
∴NE为△PCD的中位线,
∴NE∥CD且NE=
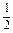 CD.
CD.又M为AB的中点,
∴AM∥CD且AM=
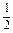 CD,
CD,∴AM∥NE且AM=NE,
∴四边形AENM为平行四边形,∴AE∥MN.
又△PAD为等腰三角形,∴AE⊥PD,∴MN⊥PD.
连接PM、MC,设AD=a,AB=2b,
∴PM2=a2+b2,CM2=a2+b2,
∴CM=PM,∴MN⊥PC.
∵PC∩PD=P,∴MN⊥平面PCD.△ABC为正三角形,
D、E分别是BC、CA的中点.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
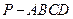 中,
中,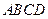 是平行四边形,
是平行四边形,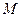 ,
,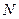 分别是
分别是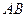 ,
,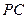 的中点.
的中点.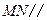 平面
平面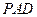 .
.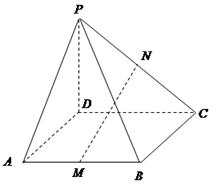
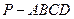 的底面边长和各侧棱长都是13,
的底面边长和各侧棱长都是13,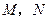 分别是
分别是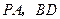 上的点且
上的点且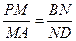 .求证:直线
.求证:直线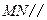 平面
平面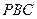

 中,
中, 是平面
是平面 上的线段,
上的线段, 平面
平面