题目内容
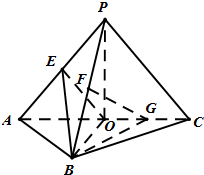
底面ABCD为矩形的四棱锥P-ABCD中,AB=
,BC=1,PA=2,侧棱PA⊥底面ABCD,E为PD的中点
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离.

| 3 |
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离.

(1)以A为原点,AB、AD、AP分别为x、y、z轴,建立空间直角坐标系如图所示
可得B(
,0,0)、C(
,1,0)、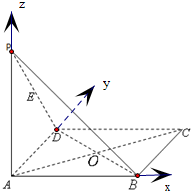 D(0,1,0)、
D(0,1,0)、
P(0,0,2)、E(0,
,1),
从而
=(
,1,0),
=(
,0,-2).
设
与
的夹角为θ,则
cosθ=
=
=
,
∴AC与PB所成角的余弦值为
(Ⅱ)由于N点在侧面PAB内,故可设N点坐标为(x,0,z),
则
=(-x,
,1-z),
由NE⊥面PAC可得,
,即
化简得
,即
,可得N点的坐标为(
,0,1),
从而侧面PAB内存在点N,使NE⊥面PAC,N点到AB和AP的距离分别为1,
.
可得B(
| 3 |
| 3 |
 D(0,1,0)、
D(0,1,0)、P(0,0,2)、E(0,
| 1 |
| 2 |
从而
| AC |
| 3 |
| PB |
| 3 |
设
| AC |
| PB |
cosθ=
| ||||
|
|
| 3 | ||
2
|
3
| ||
| 14 |
∴AC与PB所成角的余弦值为
3
| ||
| 14 |
(Ⅱ)由于N点在侧面PAB内,故可设N点坐标为(x,0,z),
则
| NE |
| 1 |
| 2 |
由NE⊥面PAC可得,
|
|
化简得
|
|
| ||
| 6 |
从而侧面PAB内存在点N,使NE⊥面PAC,N点到AB和AP的距离分别为1,
| ||
| 6 |

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
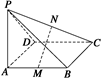
 如图,在四棱锥
如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 底面
底面 ,
, 是
是 的中点。
的中点。 ;
; 以
以 为轴旋转所围成的几何体体积。
为轴旋转所围成的几何体体积。