题目内容
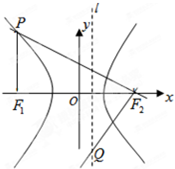
如图,F1(-c,0),F2(c,0)分别是双曲线C:
-
=1(a>0,b>0)的左,右焦点,过点F1作x轴的垂线交双曲线的上半部分于点P,过点F2作直线PF2的垂线交直线l:x=
于点Q,若点Q的坐标为(1,-4).
(Ⅰ)求双曲线C的方程;
(Ⅱ)求∠F1PF2的角平分线所在直线的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
(Ⅰ)求双曲线C的方程;
(Ⅱ)求∠F1PF2的角平分线所在直线的方程.

(Ⅰ)将点P(-c,y1)(y1>0)代入
-
=1得y1=
∴P(-c,
)
∵点Q的坐标是(1,-4),PF2⊥QF2
∴
×
=-1
∵
=1,c2=a2-b2
∴a=2,c=4,b=
=2
∴双曲线C的方程为
-
=1;
(Ⅱ)由(Ⅰ)知,F1(-4,0),F2(4,0),P(-4,6),则|PF1|=6,|PF2|=10
设∠F1PF2的角平分线所在直线的方程与x轴交于M(x,0),则由角平分线的性质可得
=
∴x=-1,∴M(-1,0)
∴∠F1PF2的角平分线所在直线的方程为
=
,即2x+y+2=0.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
∴P(-c,
| b2 |
| a |
∵点Q的坐标是(1,-4),PF2⊥QF2
∴
| ||
| -c-c |
| 0+4 |
| c-1 |
∵
| a2 |
| c |
∴a=2,c=4,b=
| c2-a2 |
| 3 |
∴双曲线C的方程为
| x2 |
| 4 |
| y2 |
| 12 |
(Ⅱ)由(Ⅰ)知,F1(-4,0),F2(4,0),P(-4,6),则|PF1|=6,|PF2|=10
设∠F1PF2的角平分线所在直线的方程与x轴交于M(x,0),则由角平分线的性质可得
| 10 |
| 6 |
| 4-x |
| x+4 |
∴x=-1,∴M(-1,0)
∴∠F1PF2的角平分线所在直线的方程为
| y-0 |
| 6-0 |
| x+1 |
| -4+1 |

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
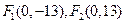 的距离的差的绝对值等于
的距离的差的绝对值等于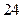 的点的轨迹是( )
的点的轨迹是( )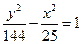
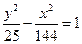

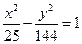
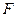 、
、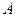 分别为双曲线
分别为双曲线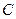 :
: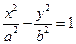
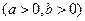 的左焦点、右顶点,点
的左焦点、右顶点,点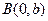 满足
满足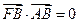 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )