题目内容
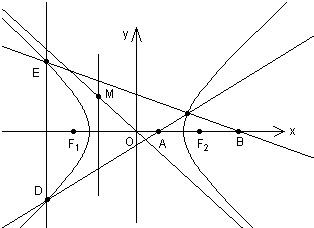
已知双曲线与椭圆
+
=1有相同焦点,且经过点(
,4).
(1)求椭圆的焦点坐标及离心率;
(2)求此双曲线的标准方程.
| x2 |
| 27 |
| y2 |
| 36 |
| 15 |
(1)求椭圆的焦点坐标及离心率;
(2)求此双曲线的标准方程.
(1)由题意得:a2=36,b2=27.
∵c2=a2-b2=9,
∴a=6,c=3,e=
=
.
∴焦点F1(0,-3),F2(0,3).
(2)设双曲线方程为
-
=1,
∵点(
,4)在曲线上,代入双曲线的方程可得m=4或m=36(舍).
∴双曲线的方程为
-
=1.
∵c2=a2-b2=9,
∴a=6,c=3,e=
| c |
| a |
| 1 |
| 2 |
∴焦点F1(0,-3),F2(0,3).
(2)设双曲线方程为
| y2 |
| m |
| x2 |
| 9-m |
∵点(
| 15 |
∴双曲线的方程为
| y2 |
| 4 |
| x2 |
| 5 |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
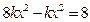 的一个焦点为
的一个焦点为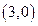 ,求
,求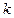 的值。
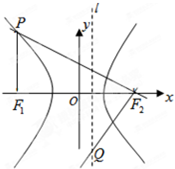
的值。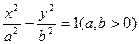 的左、右焦点分别为F1,F2,点P为该双曲线在第一象限的点,△PF1F2面积为1,且
的左、右焦点分别为F1,F2,点P为该双曲线在第一象限的点,△PF1F2面积为1,且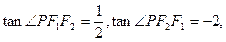 则该双曲线的方程为
则该双曲线的方程为