题目内容
【题目】如图,两座建筑物![]() ,
,![]() 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是![]() 和
和![]() ,从建筑物
,从建筑物![]() 的顶部
的顶部![]() 看建筑物
看建筑物![]() 的视角
的视角![]() .
.
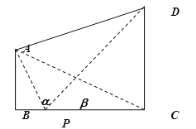
(1)求![]() 的长度;
的长度;
(2)在线段![]() 上取一点
上取一点![]() (点
(点![]() 与点
与点![]() ,
,![]() 不重合),从点
不重合),从点![]() 看这两座建筑物的视角分别为
看这两座建筑物的视角分别为![]() ,
,![]() ,问点
,问点![]() 在何处时,
在何处时,![]() 最小?
最小?
【答案】(1)![]() ;(2)
;(2)![]() 为
为![]() 时,
时,![]() 取得最小值.
取得最小值.
【解析】
(1)由题意可知![]() 是等边三角形,
是等边三角形,![]() ,根据条件直接求
,根据条件直接求![]() 的长度;
的长度;
(2)由(1)设![]() ,则
,则![]() ,分别求
,分别求![]() 和
和![]() ,然后再表示
,然后再表示![]()
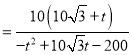 ,设
,设![]() ,利用导数求函数的最小值和
,利用导数求函数的最小值和![]() 点的位置.
点的位置.
(1)如图,作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,![]() ,设
,设![]() ,
,
由条件可知![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,![]()
.![]() .
.
答:![]() 的长度为
的长度为![]() .
.
(2)设![]() ,则
,则![]() ,
,

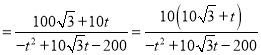 .
.
设![]() ,
,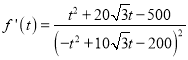 ,
,
令![]() ,因为
,因为![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是减函数;
是减函数;
当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,
所以,当![]() 时,
时,![]() 取得最小值,即
取得最小值,即![]() 取得最小值,
取得最小值,
因为![]() 恒成立,所以
恒成立,所以![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() 在
在![]() 上是增函数,所以当
上是增函数,所以当![]() 时,
时,![]() 取得最小值.
取得最小值.
答:当![]() 为
为![]() 时,
时,![]() 取得最小值.
取得最小值.

 阅读快车系列答案
阅读快车系列答案【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)有一种植户准备种植该种水果500株,且每株与它“相近”的株数都为![]() ,计划收获后能全部售出,价格为10元
,计划收获后能全部售出,价格为10元![]() ,如果收入(收入=产量×价格)不低于25000元,则
,如果收入(收入=产量×价格)不低于25000元,则![]() 的最大值是多少?
的最大值是多少?
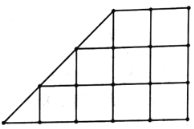
(3)该种植基地在如图所示的直角梯形地块的每个交叉点(直线的交点)处都种了一株该种水果,其中每个小正方形的边长和直角三角形的直角边长都为![]() ,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: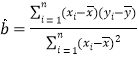 ,
,![]() .
.