题目内容
【题目】某港口某天0时至24时的水深![]() (米)随时间
(米)随时间![]() (时)变化曲线近似满足如下函数模型
(时)变化曲线近似满足如下函数模型![]() (
(![]() ).若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为( )
).若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为( )
A.16时B.17时C.18时D.19时
【答案】D
【解析】
本题是单选题,利用回代验证法,结合五点法作图以及函数的最值的位置,判断即可.
解:由题意可知,![]() 时,
时,![]() ,
,
由五点法作图可知:如果当![]() 时,函数取得最小值可得:
时,函数取得最小值可得:![]() ,可得
,可得![]() ,
,
此时函数![]() ,函数的周期为:
,函数的周期为: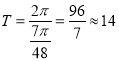 ,
,
该港口在该天0时至24时内,有且只有3个时刻水深为3米,满足,
如果当![]() 时,函数取得最小值可得:
时,函数取得最小值可得:![]() ,可得
,可得![]() ,
,
此时函数![]() ,函数的周期为:
,函数的周期为: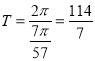 ,
,
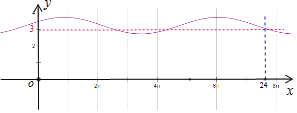
![]() 时,
时,![]() ,如图:
,如图:
该港口在该天0时至24时内,有且只有3个时刻水深为3米,不满足,
故选:D.

练习册系列答案
相关题目
【题目】下表列出了10名5至8岁儿童的体重x(单位kg)(这是容易测得的)和体积y(单位dm3)(这是难以测得的),绘制散点图发现,可用线性回归模型拟合y与x的关系:
体重x | 17.00 10.50 13.80 15.70 11.90 10.20 15.00 17.80 16.00 12.10 |
体积y | 16. 70 10.40 13.50 15.70 11.60 10.00 14.50 17.50 15.40 11.70 |
(1)求y关于x的线性回归方程![]() (系数精确到0.01);
(系数精确到0.01);
(2)某5岁儿童的体重为13.00kg,估测此儿童的体积.
附注:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,137×14=1918.00.
,137×14=1918.00.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: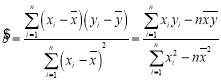 ,
,![]() .
.