题目内容
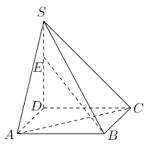
【题目】如图,四棱锥![]() 的底面是正方形,
的底面是正方形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点.
上任意一点.
(1)求证:![]() ;
;
(2)试确定点![]() 的位置,使
的位置,使![]() 与平面
与平面![]() 所成角的大小为30°.
所成角的大小为30°.
【答案】(1)证明见解析(2)当![]() 时,
时,![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]()
【解析】
(1)连结![]() ,通过证明
,通过证明![]() 平面
平面![]() ,即可得
,即可得![]() .另外可以利用空间向量证明线线垂直;
.另外可以利用空间向量证明线线垂直;
(2)由![]() ⊥平面
⊥平面![]() 可得
可得![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,在
,在![]() 中可求出
中可求出![]() 值,即可得到点
值,即可得到点![]() 的位置.另外还可以用空间向量法求线面角.
的位置.另外还可以用空间向量法求线面角.
(1)证明:连结![]() ,因为四边形
,因为四边形![]() 为正方形,
为正方形,
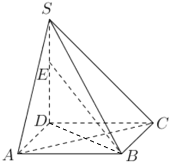
所以,![]() ,
,
又因为![]() ⊥平面
⊥平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .由
.由
![]()
![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解法一:设![]() ,因为
,因为![]() ⊥平面
⊥平面![]() ,
,
所以![]() 与平面
与平面![]() 所成角为
所成角为![]()
在![]() 中,由
中,由![]()
![]()
![]()
![]() .
.
所以,当![]() 时,
时,![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
解法2:(1)以![]() 为坐标原点,建立空间直角坐标系.
为坐标原点,建立空间直角坐标系.
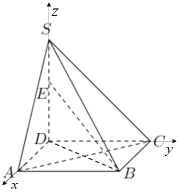
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() ,则
,则![]()
则![]() ,
,![]()
因为![]() ,
,
所以![]() ;
;
(2)取平面![]() 的一个法向量为
的一个法向量为![]()
因为![]() ,可知直线
,可知直线![]() 的一个方向向量为
的一个方向向量为![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,由题意知
,由题意知![]()
![]() .
.![]() 与
与![]() 所成的角为
所成的角为![]() ,
,
则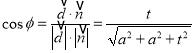 ,
,
因为![]() ,所以,
,所以,![]() ,
,
解得,![]() .
.
当![]() 时,
时,![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?