题目内容
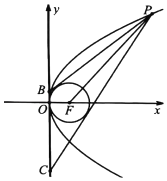
【题目】已知椭圆![]() ,倾斜角为60°的直线与椭圆分别交于A、B两点且
,倾斜角为60°的直线与椭圆分别交于A、B两点且![]() ,点C是椭圆上不同于A、B一点,则△ABC面积的最大值为_____.
,点C是椭圆上不同于A、B一点,则△ABC面积的最大值为_____.
【答案】![]()
【解析】
设直线AB的方程为![]() ,联立方程组,利用根与系数的关系及弦长公式,得到
,联立方程组,利用根与系数的关系及弦长公式,得到
![]() ,解得
,解得![]() 的值,设与直线
的值,设与直线![]() 平行且与椭圆相切的直线方程为
平行且与椭圆相切的直线方程为![]() ,联立方程组,利用
,联立方程组,利用![]() ,求得
,求得![]() 的值,再由点到直线的距离公式和三角形的面积公式,即可求解.
的值,再由点到直线的距离公式和三角形的面积公式,即可求解.
由题意,设直线AB的方程为![]() ,点 A(x1,y1),B(x2,y2),
,点 A(x1,y1),B(x2,y2),
联立方程组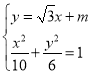 ,整理得18x2+10
,整理得18x2+10![]() mx+5m2﹣30=0,
mx+5m2﹣30=0,
所以x1+x2![]() ,x1x2
,x1x2![]() .
.
因为![]() ,即
,即![]() ,
,
代入整理得![]() ,解得
,解得![]() ,
,
不妨取:m=2,可得直线AB的方程为![]() ,
,
设与直线AB平行且与椭圆相切的直线方程为y![]() x+t,
x+t,
联立方程组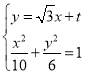 ,整理得18x2+10
,整理得18x2+10![]() tx+5t2﹣30=0,
tx+5t2﹣30=0,
由△=300t2﹣72×(5t2﹣30)=0,解得:t=±6.
取t=﹣6时,与直线AB平行且与椭圆相切的直线与直线AB的距离 ,
,
所以△ABC面积的最大值![]()
![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目