Question

【题目】已知函数．

（1）那么方程在区间上的根的个数是___________．

（2）对于下列命题：

①函数是周期函数；

②函数既有最大值又有最小值；

③函数的定义域是，且其图象有对称轴；

④在开区间上，单调递减．

其中真命题的序号为______________（填写真命题的序号）．

Answer 1

【答案】4039； ②③；

【解析】

（1）方程在区间上的根，即为在区间上的根．

（2）根据函数的周期性的定义、最值、对称性以及单调性判断可得；

解：（1），即，即，，解得，，

由于，

方程在区间上的根的个数是4039个，

（2）①函数是周期函数不正确，因为分母随着自变量的远离原点，趋向于正穷大，

所以函数图象无限靠近于轴，故不是周期函数，故①错误；

③，，则恒成立；故函数的定义域为，在函数图象上任取点，则点关于直线的对称点是

而．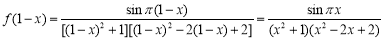

直线是函数图象的对称轴；故③正确，

②因为有最值，在上单调递增，在上单调递减，所以，从而（当且仅当取等号），所以既有最大值又有最小值；故②正确；

④因为函数在与时，，故在开区间上，不可能单调递减．故④错误；

故正确的有②③．

故答案为：（1）、4039；（2）、②③；