题目内容

8．2sin2x-sinxcosx-cos2x=1的解集是{x|x=kπ+arctan2或x=kπ-$\frac{π}{4}$，k∈Z}．

分析 首先，化简所给方程，然后，分解因式，从而确定其解集．

解答 解：∵2sin2x-sinxcosx-cos2x=1=sin2x+cos2x
∴six2x-sinxcosx-2cos2x=0，
∴（sinx-2cosx）（sinx+cosx）=0
sinx-2cosx=0，或sinx+cosx=0
tanx=2或tanx=-1
解集是{x|x=kπ+arctan2或x=kπ-$\frac{π}{4}$，k∈Z}．
故答案为：{x|x=kπ+arctan2或x=kπ-$\frac{π}{4}$，k∈Z}．

点评 本题重点考查了同角三角函数基本关系式、反三角函数等知识，属于中档题．

练习册系列答案
相关题目
8．已知p：-2≤x≤10，q：x2-2x+1-m2≤0（m＞0），若￢p是￢q的充分不必要条件，求实数m的取值范围．
9．已知a=log${\;}_{\frac{1}{2}}$2，b=20.6，c=0.62，则a，b，c的大小关系为a＜c＜b．
16．曲线y=ax3-2bx+1在点（1，f（1））处的切线方程为y=-x+2，则a+2b=（　　）
A．-1B．1C．2D．3
3．已知函数 f （x） 对任意x∈R都有f（x）+f（1-x）=2011．
（1）求 f（$\frac{1}{2}$）的值．
（2）数列{an} 满足：an=f（0）+f（$\frac{1}{n}$）+f（$\frac{2}{n}$）+…+f（$\frac{n-2}{n}$）+f（$\frac{n-1}{n}$）+f（1），求数列{$\frac{{{2a}_{n}a}^{n}}{2011}$}的前n项和Sn．
（3）若Tn=$\frac{1}{{{a}_{1}}^{2}}$+$\frac{1}{{{a}_{2}}^{2}}$+…+$\frac{1}{{{a}_{n}}^{2}}$，证明：${T_n}＜\frac{4}{{{{2011}^2}}}$．
13．P为平面ABCD外一点，E∈PB，F∈AC，且$\frac{PE}{EB}$=$\frac{CF}{FA}$，求证：EF∥平面PCD．
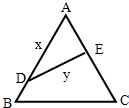20．如图，某公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．
（Ⅰ）设AD=x，DE=y，求y关于x的函数关系式；
（Ⅱ）如果DE是灌溉水管，我们希望它最短，则DE的位置应在哪里？请予以证明．
17．判断下列命题属于全称命题还是特称命题，并用数学量词符号改写下列命题：
（1）任意的m＞1方程x2-2x+m=0无实数根；
（2）存在一对实数 x，y，使2x+3y+3＞0成立；
（3）存在一个三角形没有外接圆；
（4）实数的平方大于等于0．
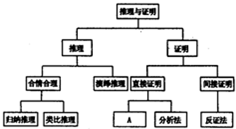18．如图是教材选修1-2中《推理与证明》一章的知识结构图，请把A处填入适当的方法综合法．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网