题目内容
【题目】多面体![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在平面
在平面![]() 上的射影
上的射影![]() 是线段
是线段![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(Ⅰ)过E作EO∥A1A交AB于O,连接CO,证明四边形OEC1C是平行四边形,推出C1E⊥面ABB1A1,得到CO⊥面ABB1A1,然后证明面ABC⊥面ABB1A1;
(Ⅱ)以点O为坐标原点建立空间直角坐标系,求出面AB1C1的法向量,底面A1B1BA的法向量,利用空间向量的数量积求解即可.
试题解析:
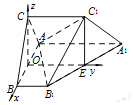
(1)证明:过E作EO∥![]() A交AB于O,连接CO,
A交AB于O,连接CO,
由梯形的中位线知: ![]() ,
,
∴![]() ,又
,又![]() ,
,
故四边形OE![]() C是平行四边形,
C是平行四边形,
∴![]() E⊥面
E⊥面![]() ,则CO⊥面
,则CO⊥面![]() ,
,
又CO在面ABC内,
∴面ABC⊥面![]() ;
;
(2)如图以点O为坐标原点建立空间直角坐标系, ![]() ,
,
![]() 设面
设面![]() 的法向量为
的法向量为![]() ,
,
则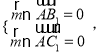 即
即![]() .
.
不妨令![]() ,得
,得![]() .
.
设面![]() 的法向量为
的法向量为![]()
则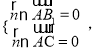 即
即![]() .
.
不妨令![]() ,得
,得![]() .
.
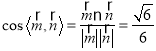 .
.
所求二面角的平面角为锐角,故余弦值![]() .
.

练习册系列答案
相关题目