题目内容
已知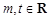 ,函数
,函数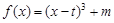 .
.
(1)当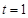 时,若
时,若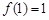 ,求函数
,求函数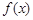 的单调区间;
的单调区间;
(2)若关于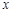 的不等式
的不等式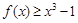 在区间
在区间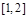 上有解,求
上有解,求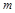 的取值范围;
的取值范围;
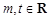 ,函数
,函数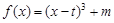 .
.(1)当
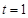 时,若
时,若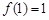 ,求函数
,求函数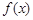 的单调区间;
的单调区间;(2)若关于
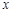 的不等式
的不等式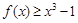 在区间
在区间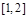 上有解,求
上有解,求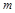 的取值范围;
的取值范围;解析:(1)因为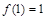 ,所以
,所以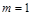 , ……………………2分
, ……………………2分
则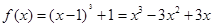 , 而
, 而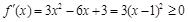 恒成立,
恒成立,
所以函数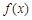 的单调递增区间为
的单调递增区间为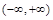 . ……………………6分
. ……………………6分
(2)不等式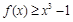 在区间
在区间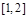 上有解,
上有解,
即 不等式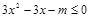 在区间
在区间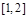 上有解,
上有解,
即 不等式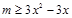 在区间
在区间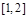 上有解,
上有解,
等价于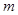 不小于
不小于 在区间
在区间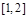 上的最小值. ……………………8分
上的最小值. ……………………8分
因为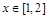 时,
时,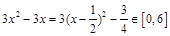 ,
,
所以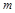 的取值范围是
的取值范围是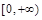 . ……………………11分
. ……………………11分
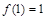 ,所以
,所以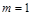 , ……………………2分
, ……………………2分则
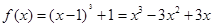 , 而
, 而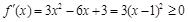 恒成立,
恒成立,所以函数
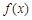 的单调递增区间为
的单调递增区间为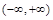 . ……………………6分
. ……………………6分(2)不等式
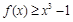 在区间
在区间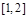 上有解,
上有解,即 不等式
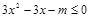 在区间
在区间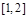 上有解,
上有解,即 不等式
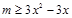 在区间
在区间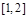 上有解,
上有解,等价于
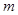 不小于
不小于 在区间
在区间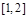 上的最小值. ……………………8分
上的最小值. ……………………8分因为
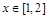 时,
时,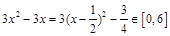 ,
,所以
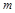 的取值范围是
的取值范围是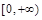 . ……………………11分
. ……………………11分本试题主要考查了导数在研究函数中的运用。
(1)因为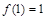 ,所以
,所以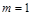 ,则
,则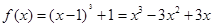 , 而
, 而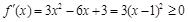 恒成立,所以函数
恒成立,所以函数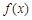 的单调递增区间为
的单调递增区间为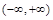 .
.
(2)不等式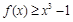 在区间
在区间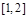 上有解,
上有解,
即 不等式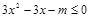 在区间
在区间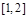 上有解,
上有解,
即 不等式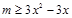 在区间
在区间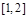 上有解,
上有解,
运用转化与划归思想得到结论。
(1)因为
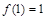 ,所以
,所以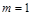 ,则
,则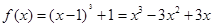 , 而
, 而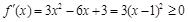 恒成立,所以函数
恒成立,所以函数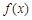 的单调递增区间为
的单调递增区间为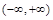 .
.(2)不等式
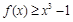 在区间
在区间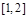 上有解,
上有解,即 不等式
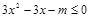 在区间
在区间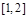 上有解,
上有解,即 不等式
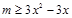 在区间
在区间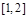 上有解,
上有解,运用转化与划归思想得到结论。

练习册系列答案
相关题目
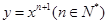 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为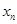 ,令
,令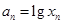 ,则
,则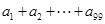 的值为
的值为 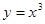 在点
在点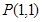 的切线方程为 .
的切线方程为 .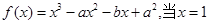 时,有极值10,则
时,有极值10,则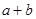 的值为
的值为 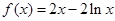
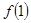 )的切线方程
)的切线方程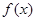 的极值
的极值 ,如果存在曲线上的点
,如果存在曲线上的点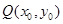 ,且
,且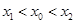 ,使得曲线在点
,使得曲线在点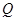 处的切线
处的切线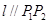 ,则称
,则称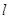 为弦
为弦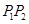 的陪伴切线.
的陪伴切线.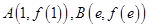 ,试求弦
,试求弦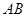 的陪伴切线
的陪伴切线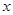 个月,顾客对某种商品的需求总量
个月,顾客对某种商品的需求总量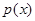 (单位:件)与
(单位:件)与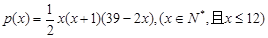 .该商品第
.该商品第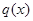 (单位:元)与x的近似关系是:
(单位:元)与x的近似关系是: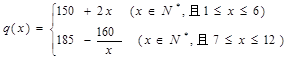
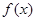 件与
件与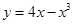 在点
在点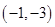 处的切线方程是____________
处的切线方程是____________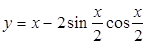 ,则
,则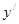 =
=