题目内容
.已知函数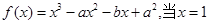 时,有极值10,则
时,有极值10,则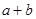 的值为
的值为
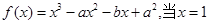 时,有极值10,则
时,有极值10,则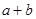 的值为
的值为 0或7
解:由f(x)=x3+ax2+bx+a2,
得f′(x)=3x2+2ax+b,
f′(1)="0"
f(1)=0 ,即 2a+b=3=0, a2+a+b+1=10 ,
解得 a=4, b=-11 或 a="-3" ,b=3 (经检验应舍去),
a+b=4-11=-7,
得f′(x)=3x2+2ax+b,
f′(1)="0"
f(1)=0 ,即 2a+b=3=0, a2+a+b+1=10 ,
解得 a=4, b=-11 或 a="-3" ,b=3 (经检验应舍去),
a+b=4-11=-7,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
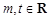 ,函数
,函数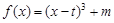 .
.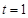 时,若
时,若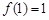 ,求函数
,求函数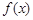 的单调区间;
的单调区间;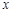 的不等式
的不等式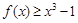 在区间
在区间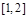 上有解,求
上有解,求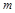 的取值范围;
的取值范围;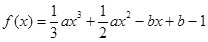 在
在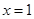 处的切线与
处的切线与 轴平行,若
轴平行,若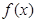 的图象经过四个象限,则实数
的图象经过四个象限,则实数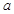 的取值范围是 。
的取值范围是 。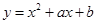 在点
在点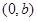 处的切线方程是
处的切线方程是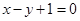 ,则( )
,则( )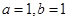
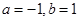
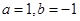
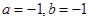
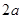 的正方形铁皮的四个角各截去一个边长为
的正方形铁皮的四个角各截去一个边长为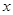 的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度
的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度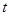 ,问:
,问: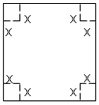
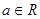 ,函数
,函数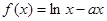 .
.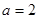 ,求函数
,求函数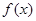 的单调区间;
的单调区间;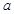 的取值范围。
的取值范围。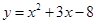 在与直线
在与直线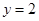 的交点处的切线方程为 .
的交点处的切线方程为 .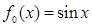 ,
,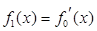 ,
,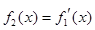 ,…,
,…, ,
,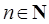 ,则
,则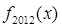 =( )
=( )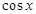
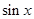
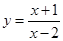 在x=1处的切线与直线
在x=1处的切线与直线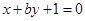 平行,则实数b的值为
平行,则实数b的值为