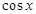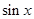题目内容
某商场预计2013年1月份起前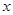 个月,顾客对某种商品的需求总量
个月,顾客对某种商品的需求总量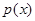 (单位:件)与
(单位:件)与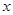 的关系近似地满足:
的关系近似地满足: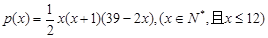 .该商品第
.该商品第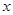 月的进货单价
月的进货单价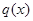 (单位:元)与x的近似关系是:
(单位:元)与x的近似关系是:
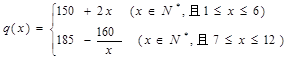
(1)写出今年第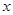 月的需求量
月的需求量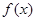 件与
件与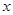 的函数关系式;
的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2013年第几月份销售该商品的月利润最大,最大月利润为多少元?
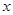 个月,顾客对某种商品的需求总量
个月,顾客对某种商品的需求总量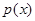 (单位:件)与
(单位:件)与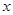 的关系近似地满足:
的关系近似地满足: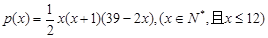 .该商品第
.该商品第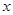 月的进货单价
月的进货单价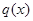 (单位:元)与x的近似关系是:
(单位:元)与x的近似关系是: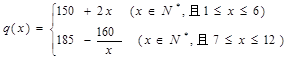
(1)写出今年第
 月的需求量
月的需求量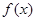 件与
件与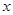 的函数关系式;
的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2013年第几月份销售该商品的月利润最大,最大月利润为多少元?
(1)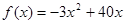
(2)商场2011年第5月份的月利润最大,最大利润为3125元
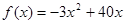
(2)商场2011年第5月份的月利润最大,最大利润为3125元
本试题主要是考查了函数在实际生活中的运用,主要是分段函数的运用。
(1)根据前x个月的总量,作差法得到第x个月的销售商品的需求量,然后得到关系式。
(2)根据题意设出变量,并能利用变量得到关于利润的函数关系式,借助于分段函数的性质,逐一求解最值,再比较大小得到结论。
解:(1)当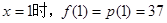 …………1分
…………1分
当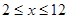 ,且
,且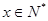 时,
时,
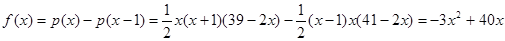 …………4分
…………4分
验证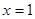 符合
符合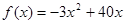 (x∈N*,且
(x∈N*,且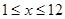 ). …………5分
). …………5分
(2)该商场预计第x月销售该商品的月利润为:
g(x)=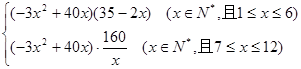
=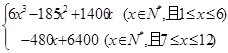
…………8分
当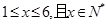 时
时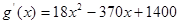 ,
,
令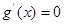 ,解得
,解得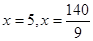 (舍去). …………9分
(舍去). …………9分
当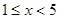 时,g′(x) >0,当
时,g′(x) >0,当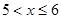 时,g′(x) <0,
时,g′(x) <0,
∴当x=5时,g(x)max=g(5)=3125(元). …………11分
当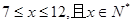 时,
时,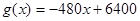 是减函数,
是减函数,
当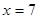 时,
时,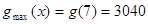 (元) …………13分
(元) …………13分
综上,商场2011年第5月份的月利润最大,最大利润为3125元. …………14分
(1)根据前x个月的总量,作差法得到第x个月的销售商品的需求量,然后得到关系式。
(2)根据题意设出变量,并能利用变量得到关于利润的函数关系式,借助于分段函数的性质,逐一求解最值,再比较大小得到结论。
解:(1)当
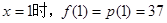 …………1分
…………1分当
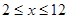 ,且
,且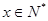 时,
时,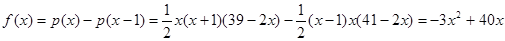 …………4分
…………4分验证
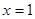 符合
符合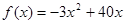 (x∈N*,且
(x∈N*,且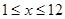 ). …………5分
). …………5分(2)该商场预计第x月销售该商品的月利润为:
g(x)=
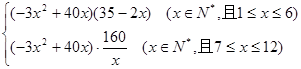
=
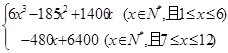
…………8分
当
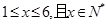 时
时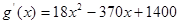 ,
,令
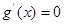 ,解得
,解得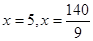 (舍去). …………9分
(舍去). …………9分当
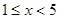 时,g′(x) >0,当
时,g′(x) >0,当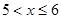 时,g′(x) <0,
时,g′(x) <0,∴当x=5时,g(x)max=g(5)=3125(元). …………11分
当
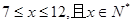 时,
时,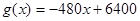 是减函数,
是减函数,当
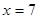 时,
时,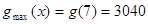 (元) …………13分
(元) …………13分综上,商场2011年第5月份的月利润最大,最大利润为3125元. …………14分

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,函数
,函数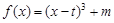 .
.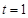 时,若
时,若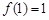 ,求函数
,求函数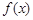 的单调区间;
的单调区间;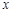 的不等式
的不等式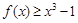 在区间
在区间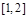 上有解,求
上有解,求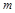 的取值范围;
的取值范围;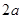 的正方形铁皮的四个角各截去一个边长为
的正方形铁皮的四个角各截去一个边长为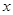 的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度
的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度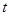 ,问:
,问: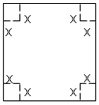
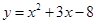 在与直线
在与直线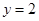 的交点处的切线方程为 .
的交点处的切线方程为 . 的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?
的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?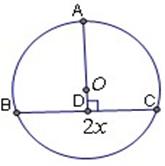
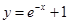 在
在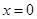 处的切线方程为_____________.
处的切线方程为_____________.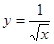 在点
在点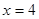 处的导数是
处的导数是 
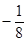
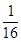 (
(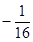
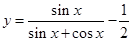 在点
在点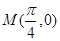 处的切线的斜率为 。
处的切线的斜率为 。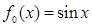 ,
,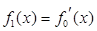 ,
,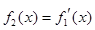 ,…,
,…, ,
,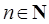 ,则
,则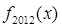 =( )
=( )