题目内容
已知函数f(x)=
若f(2-x2)>f(x),则实数x的取值范围是( )
若f(2-x2)>f(x),则实数x的取值范围是( )| A．(-∞,-1)∪(2,+∞) |
| B．(-∞,-2)∪(1,+∞) |
| C．(-1,2) |
| D．(-2,1) |
D
画出函数f(x)的大致图象如图,
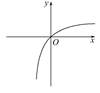
由图形易知f(x)在R上为单调递增函数,因此由f(2-x2)>f(x)可知2-x2>x,即x2+x-2<0,解得-2<x<1,即实数x的取值范围是(-2,1).
由图形易知f(x)在R上为单调递增函数,因此由f(2-x2)>f(x)可知2-x2>x,即x2+x-2<0,解得-2<x<1,即实数x的取值范围是(-2,1).
练习册系列答案
相关题目
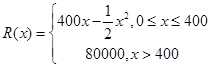，其中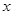
是仪器的月产量．
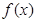表示为月产量
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
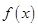，若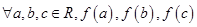
为某一三角形的三边长，则称
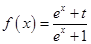是“可构造三角形函数”，则实数t的取值范围是（ ）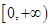
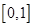
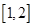
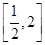
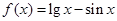，则
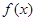在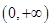
上的零点个数为（ ）