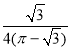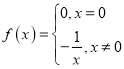题目内容
【题目】已知函数![]() ,
,![]() 为
为![]() 的导数.
的导数.
(1)求![]() 的最值;
的最值;
(2)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)最小值为![]() ,无最大值(2)
,无最大值(2)![]()
【解析】
(1)本题首先可求出![]() 以及
以及![]() ,然后绘出函数
,然后绘出函数![]() 、
、![]() 以及
以及![]() 的图像,结合图像即可得出结果;
的图像,结合图像即可得出结果;
(2)本题首先可判断出函数![]() 是增函数和奇函数,然后根据增函数和奇函数的性质将
是增函数和奇函数,然后根据增函数和奇函数的性质将![]() 转化为
转化为![]() ,最后令
,最后令![]() ,通过求解函数
,通过求解函数![]() 的最值即可得出结果.
的最值即可得出结果.
(1)因为函数![]() ,
,
所以![]() ,
,![]() ,
,
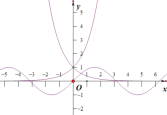
如图,分别绘出函数![]() 、
、![]() 以及
以及![]() 的图像,
的图像,
结合函数图像,易知:
当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 是增函数,
是增函数,
当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 是减函数,
是减函数,
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 取最小值,
取最小值,![]() ,
,
故![]() 有最小值,最小值为
有最小值,最小值为![]() ,无最大值,
,无最大值,
(2)因为![]() ,
,![]()
所以函数![]() 是奇函数,
是奇函数,
因为由(1)可知,![]() ,
,
所以函数![]() 是增函数,
是增函数,
故![]() ,即
,即![]() ,
,![]() ,
,
化简得![]() ,
,
因为![]() 对
对![]() 恒成立,
恒成立,
所以![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 是减函数,
是减函数,
当![]() 时,
时,![]() ,函数
,函数![]() 是增函数,
是增函数,
当![]() 时,
时,![]() ,函数
,函数![]() 取最大值,
取最大值,![]() ,
,
因为![]() 恒成立,所以
恒成立,所以![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】为调查某地区被隔离者是否需要社区非医护人员提供帮助,用简单随机抽样方法从该地区调查了500位被隔离者,结果如下:
性别 是否需要 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区被隔离者中,需要社区非医护人员提供帮助的被隔离者的比例;
(2)能否有99%的把握认为该地区的被隔离者是否需要社区非医护人员提供帮助与性别有关?