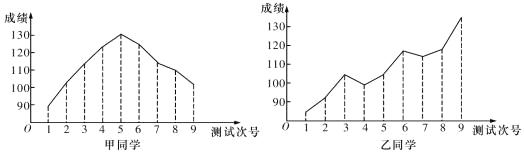
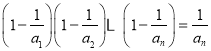题目内容
【题目】2019年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善生存环境质量.某部门在某小区年龄处于区间![]() 内的人中随机抽取
内的人中随机抽取![]() 人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
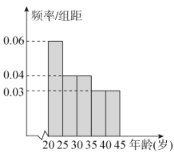
(1)求![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
(3)从年龄段在![]() 的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间
的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间![]() 中的概率.
中的概率.
组数 | 分组 | “环保族”人数 | 占本组频率 |
第一组 |
| 45 | 0.75 |
第二组 |
| 25 |
|
第三组 |
|
| 0.5 |
第四组 |
| 3 | 0.2 |
第五组 |
| 3 | 0.1 |
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)31;(3)
;(2)31;(3)![]() .
.
【解析】
(1)根据频率分布直方图和表中统计数据计算可得;
(2)根据频率分布直方图计算出平均数即可;
(3)根据古典概型的概率计算公式计算可得;
解:(1)对于第一组,人数为![]() ,占总人数
,占总人数![]() ,故总人数
,故总人数![]() 人,所以
人,所以![]() ,
,![]() ,
,![]() .
.
(2)设这![]() 人年龄的平均值为
人年龄的平均值为![]() ,所以
,所以![]() .
.
(3)易知采用分层抽样法抽取的9人中,在![]() 内的有5人,在
内的有5人,在![]() 内的有4人,选取2名记录员的可能情况共有
内的有4人,选取2名记录员的可能情况共有![]() 种,均在
种,均在![]() 内的有
内的有![]() 种,恰有一个在
种,恰有一个在![]() 内的有
内的有![]() 种,故所求概率
种,故所求概率![]() .
.

【题目】某同学对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,他在4月份的![]() 天中随机挑选了
天中随机挑选了![]() 天进行研究,且分别记录了每天昼夜温差与每天每
天进行研究,且分别记录了每天昼夜温差与每天每![]() 颗种子浸泡后的发芽数,得到如下数据:
颗种子浸泡后的发芽数,得到如下数据:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从这![]() 天中任选
天中任选![]() 天,若选取的是4月1日与4月30日的两组数据.请根据这
天,若选取的是4月1日与4月30日的两组数据.请根据这![]() 天中的另外
天中的另外![]() 天的数据,求出
天的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
参考公式和数据:线性回归方程![]() ,
,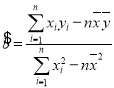 ,
,![]() ,
,![]() ,
,![]() .
.