题目内容
4.三棱锥的四个面中,设Rt△的个数为n,若当n取最大值时,该三棱锥的最大棱长为(n+1)2-2n,则该三棱锥外接球的表面积为81π.分析 由题意画出图形,可知三棱锥P-ABC的四个面中,Rt△的个数n的最大值为4,结合直径所对圆周角为直角可知最大棱PC为三棱锥外接球的直径,则该三棱锥外接球的表面积可求.
解答 解:如图,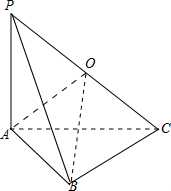
三棱锥P-ABC的四个面中,Rt△的个数n的最大值为4,
此时PA⊥面ABC,∠ABC=90°,则∠PBC=90°,
三棱锥的最大边为PC,
由题意可得PC=52-24=9,其外接球的半径为$\frac{1}{2}PC=\frac{9}{2}$,
∴外接球的表面积为S=4π•$(\frac{9}{2})^{2}=81π$.
故答案为:81π.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.已知角A,B,C为△ABC的三个内角,那么$\frac{1}{2}$[cos(A-B)-cos(A+B)]sin2C的取值范围是( )
| A. | (0,$\frac{20}{27}$] | B. | (0,$\frac{16}{27}$] | C. | (0,$\frac{9}{16}$] | D. | (0,$\frac{7}{16}$] |
19.执行如图所示的程序框图,则输出的S的值为( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |