题目内容
8.函数y=$\frac{{|{sinx}|}}{sinx}+\frac{cosx}{{|{cosx}|}}+\frac{{2|{tanx}|}}{tanx}$的值域是( )| A. | {-2,4} | B. | {-2,0,4} | C. | {-2,0,2,4} | D. | {-4,-2,0,4} |
分析 通过角所在象限,求出函数值即可.
解答 解:x在第一象限,函数y=$\frac{{|{sinx}|}}{sinx}+\frac{cosx}{{|{cosx}|}}+\frac{{2|{tanx}|}}{tanx}$=4.
x在第二象限,函数y=$\frac{{|{sinx}|}}{sinx}+\frac{cosx}{{|{cosx}|}}+\frac{{2|{tanx}|}}{tanx}$=-2.
x在第三象限,函数y=$\frac{{|{sinx}|}}{sinx}+\frac{cosx}{{|{cosx}|}}+\frac{{2|{tanx}|}}{tanx}$=0.
x在第四象限,函数y=$\frac{{|{sinx}|}}{sinx}+\frac{cosx}{{|{cosx}|}}+\frac{{2|{tanx}|}}{tanx}$=-2.
函数y=$\frac{{|{sinx}|}}{sinx}+\frac{cosx}{{|{cosx}|}}+\frac{{2|{tanx}|}}{tanx}$的值域是:{-2,0,4}.
故选:B.
点评 本题考查三角函数的化简求值,基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.已知数列{an}的前n项和为Sn,且Sn=n2+1,则下列结论正确的是( )
| A. | an=2n-1 | B. | an=2n+1 | C. | an=$\left\{{\begin{array}{l}{2(n=1)}\\{2n-1(n>1)}\end{array}}\right.$ | D. | an=$\left\{{\begin{array}{l}{2(n=1)}\\{2n+1(n>1)}\end{array}}\right.$ |
13.已知x∈(-$\frac{π}{2}$,0),且cosx=$\frac{4}{5}$,则sin2x=( )
| A. | $\frac{24}{25}$ | B. | $\frac{12}{25}$ | C. | -$\frac{24}{25}$ | D. | -$\frac{12}{25}$ |
18.已知函数f(x)=$\frac{3-m•{3}^{x}}{{3}^{x}}$,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[-$\frac{1}{4}$,1]上的最大值为2,若对任意x1∈[-1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )
| A. | (-∞,-$\frac{2}{3}$] | B. | (-∞,$\frac{1}{3}$] | C. | [$\frac{1}{3}$,+∞) | D. | [-$\frac{1}{3}$,+∞] |
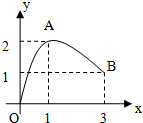 如图,函数f(x)的图象是曲线段OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f[$\frac{1}{f(3)}$]的值为2.
如图,函数f(x)的图象是曲线段OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f[$\frac{1}{f(3)}$]的值为2.