题目内容
16.已知数列{an}的通项公式an=33-6n,Sn=|a1|+|a2|+…+|an|,则S9=123.分析 令an=33-6n≥0,解得n≤5.设数列{an}的前n项和为Tn,可得Tn=-3n2+30n.因此当n≥6时,Sn=a1+a2+…+a5-a6-…-an=2T5-Tn.
解答 解:令an=33-6n≥0,解得n≤5.
设数列{an}的前n项和为Tn,则Tn=$\frac{n(27+33-6n)}{2}$=-3n2+30n.
∴当n≥6时,
Sn=|a1|+|a2|+…+|an|=a1+a2+…+a5-a6-…-an
=2T5-Tn
=2(-3×52+30×5)-(-3n2+30n),
=3n2-30n+150.
∴S9=3×92-30×9+150=123.
故答案为:123.
点评 本题考查了等差数列的通项公式及其前n项和公式、数列的单调性、含绝对值数列求和问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
6.已知正项数列{an}满足a1=1,(n+2)an+12-(n+1)a${\;}_{n}^{2}$+anan+1=0,则它的通项公式为( )
| A. | an=$\frac{1}{n+1}$ | B. | an=$\frac{2}{n+1}$ | C. | an=$\frac{n+1}{2}$ | D. | an=n |
4.2008年5月12日,四川汶川地区发生里氏8.0级特大地震.在随后的几天中,地震专家对汶川地区发生的余震进行了监测.记录的部分数据如下表:
(注:地震强度是指地震时释放的能量)
(1)画出震级(y)随地震强度(x)的变化散点图;
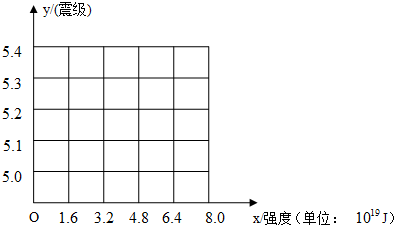
(2)根据散点图,从函数y=kx+b,y=algx+b,y=a•10x+b中选取一个函数描述震级y随地震强度x的变化关系;
(3)四川汶川地区发生里氏8.0级特大地震时释放的能量约是多少?(取lg2=0.3)
| 强度(J) | 1.6×1019 | 3.2×1019 | 4.5×1019 | 6.4×1019 |
| 震级(里氏) | 5.0 | 5.2 | 5.3 | 5.4 |
(1)画出震级(y)随地震强度(x)的变化散点图;

(2)根据散点图,从函数y=kx+b,y=algx+b,y=a•10x+b中选取一个函数描述震级y随地震强度x的变化关系;
(3)四川汶川地区发生里氏8.0级特大地震时释放的能量约是多少?(取lg2=0.3)
11.自点A(1,3)作圆(x+3)2+(y-2)2=1的切线,则切线长为( )
| A. | 4 | B. | $\sqrt{17}$ | C. | $\sqrt{10}$ | D. | 5 |
8.函数y=$\frac{{|{sinx}|}}{sinx}+\frac{cosx}{{|{cosx}|}}+\frac{{2|{tanx}|}}{tanx}$的值域是( )
| A. | {-2,4} | B. | {-2,0,4} | C. | {-2,0,2,4} | D. | {-4,-2,0,4} |
5.下列关系中,具有相关关系的是( )
(1)名师出高徒; (2)球的体积与该球的半径之间的关系;(3)苹果的产量与气候之间的关系;(4)身高与体重之间的关系;(5)出租车费与行驶的里程;(6)乌鸦叫,没好兆.
(1)名师出高徒; (2)球的体积与该球的半径之间的关系;(3)苹果的产量与气候之间的关系;(4)身高与体重之间的关系;(5)出租车费与行驶的里程;(6)乌鸦叫,没好兆.
| A. | (1)(3)(4) | B. | (1)(2)(4) | C. | (2)(5)(6) | D. | (3)(4)(5) |