题目内容
18.已知函数f(x)=$\frac{3-m•{3}^{x}}{{3}^{x}}$,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[-$\frac{1}{4}$,1]上的最大值为2,若对任意x1∈[-1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )| A. | (-∞,-$\frac{2}{3}$] | B. | (-∞,$\frac{1}{3}$] | C. | [$\frac{1}{3}$,+∞) | D. | [-$\frac{1}{3}$,+∞] |
分析 由已知函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[-$\frac{1}{4}$,1]上的最大值为2,先求出a值,进而求出两个函数在指定区间上的最小值,结合已知,分析两个最小值的关系,可得答案.
解答 解:∵函数f(x)=$\frac{3-m•{3}^{x}}{{3}^{x}}$=31-x-m,
当x1∈[-1,2]时,f(x1)∈[$\frac{1}{3}$-m,9-m];
∵t=x2+x+2的图象是开口朝上,且以直线x=-$\frac{1}{2}$为对称轴的抛物线,
故x∈[-$\frac{1}{4}$,1]时,t∈[$\frac{29}{16}$,4],
若函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[-$\frac{1}{4}$,1]上的最大值为2,
则a=2,
即g(x)=log2(x2+x+2),
当x2∈[0,3]时,g(x2)∈[1,log214],
若对任意x1∈[-1,2],存在x2∈[0,3],使得f(x1)≥g(x2),
则$\frac{1}{3}$-m≥1,
解得m∈(-∞,-$\frac{2}{3}$],
故选:A.
点评 本题考查的知识点是二次函数的图象和性质,指数函数的图象和性质,对数函数的图象和性质,难度中档.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
8.函数y=$\frac{{|{sinx}|}}{sinx}+\frac{cosx}{{|{cosx}|}}+\frac{{2|{tanx}|}}{tanx}$的值域是( )
| A. | {-2,4} | B. | {-2,0,4} | C. | {-2,0,2,4} | D. | {-4,-2,0,4} |
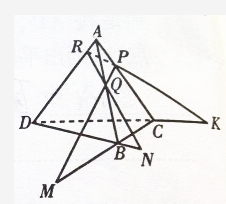 在四面体ABCD中,作截面PQR.若PQ,CB的延长线交于点M,RQ,DB的延长线交于点N,RP,DC的延长线交于点K.求证:M,N,K三点共线.
在四面体ABCD中,作截面PQR.若PQ,CB的延长线交于点M,RQ,DB的延长线交于点N,RP,DC的延长线交于点K.求证:M,N,K三点共线.