题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的极值点;
的极值点;
(2)若函数![]() 在区间
在区间![]() 上恒有
上恒有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() ,且
,且![]() ,在(2)的条件下,证明数列
,在(2)的条件下,证明数列![]() 是单调递增数列.
是单调递增数列.
【答案】(Ⅰ)![]() 的极大值点为
的极大值点为![]() ,极小值点为
,极小值点为![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】试题分析:(1)求导,利用导函数的零点,研究导函数的符号变化,进而确定函数的极值点;(2)求导、作差、分离常数,将问题转化为![]() ,
, ![]() ,再转化为求函数的最值问题;(3)利用数学归纳法进行证明.
,再转化为求函数的最值问题;(3)利用数学归纳法进行证明.
试题解析:(1)当![]() 时,
时, ![]() ,
,
![]()
![]() .
.
令![]() 得:
得: ![]() .
.
又![]() ,且
,且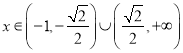 时,
时, ![]() ,
, 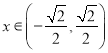 时,
时, ![]() .
.
所以,函数![]() 的极大值点为
的极大值点为![]() ,极小值点为
,极小值点为![]() .
.
(2)因为![]() ,由
,由![]() ,得
,得![]() ,
,
即![]() ,
, ![]() .
.
又![]() (∵
(∵![]() ),∴
),∴![]() .
.
(3)①当![]() 时,
时, ![]() ,又
,又![]()
![]() , ∴
, ∴![]() ,且
,且![]() ,
,
∴![]()
![]()
![]() .
.
∴![]() ,即当
,即当![]() 时结论成立.
时结论成立.
②假设当![]() 时,有
时,有![]() ,且
,且![]() ,则当
,则当![]() 时,
时,
![]()
![]()
![]() .
.
∴![]() , 即当
, 即当![]() 时结论成立.
时结论成立.
由①,②知数列![]() 是单调递增数列.
是单调递增数列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:
空气质量指数 |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 |
|
|
|
|
|
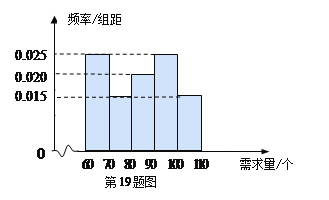
(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成頻率分布直方图:
的值,并完成頻率分布直方图:
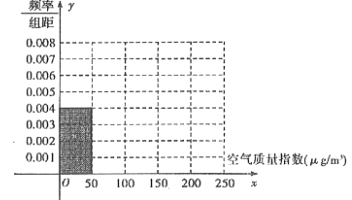
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,从中任意选取
天,从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.