题目内容
【题目】（本小题满分12分）如图所示，一根水平放置的长方体枕木的安全负荷与它的厚度d的平方和宽度a的乘积成正比，同时与它的长度
的平方成反比．
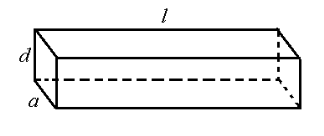
（1）在a＞d＞0的条件下，将此枕木翻转90°（即宽度变为了厚度），枕木的安全负荷会发生变化吗？变大还是变小？
（2）现有一根横截面为半圆（半圆的半径为R=
）的柱形木材，用它截取成横截面为长方形的枕木，其长度即为枕木规定的长度l，问横截面如何截取，可使安全负荷最大？
【答案】（1）变大；（2）当宽
，高
时，安全负荷最大．
【解析】
试题分析：（1）设安全负荷为
，求出翻转90°后的表达式，然后求解比值的最大值．
（2）设截取的宽为a（
），高为d，
，得到安全负荷为
，令
利用函数的导数求解最大值即可．
试题解析：设安全负荷为,
翻转90°后
,
可得： 
,
当a＞d＞0时，
1 ．此时枕木的安全负荷变大．
（2）设截取的宽为a（0＜a＜2
），高为d，
…6分
其长度l及k为定值，安全负荷为
令
此时
由
,可得
∴
所以当宽时，
取得取大值，此时高，
所以，当宽，高时，安全负荷最大
练习册系列答案
相关题目
